Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Теорема про зміну кінетичної енергії точки

Знайдемо залежність, якою пов’язані кінетична енергія і робота сили. З цією метою розглянемо матеріальну точку з масою m, яка переміщується з положення М ₀, де вона має швидкість v ₀, в положення М ₁, де її швидкість v ₁.

Для знаходження вказаної залежності звернемось до основного закону динаміки 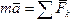. Проектуючи обидві його частини на дотичну Мτ до траєкторії точки М, спрямовану в бік руху точки, одержимо

.

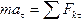Дотичне прискорення, яке входить в одержаний вираз, покажемо у вигляді

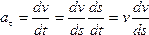. Тоді .

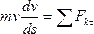Помножимо обидві частини цієї рівності на ds і внесемо m під знак диференціала. Оскільки 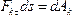, де 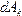- елементарна робота сили 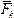, одержимо вираз теореми про зміну кінетичної енергії точки в диференціальній формі:

.

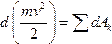Проінтегрувавши обидві частини цієї рівності в межах, які відповідають величинам змінних в точках М ₀ і М ₁, знайдемо остаточно

.

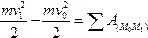Одержане рівняння є аналітичним виразом теореми про зміну кінетичної енергії точки в інтегральній формі: зміна кінетичної енергії точки при деякому її переміщенні дорівнює алгебраїчній сумі робот усіх сил, які діють на точку на тому ж переміщенні.

Теорема про зміну кінетичної енергії дозволяє, знаючи, як при русі точки змінюється її швидкість, визначити роботу сил (перша задача динаміки) або, знаючи роботу сил, визначити, як змінюється при русі швидкість точки (друга задача динаміки).

При розв’язанні другої задачі, коли задані сили, треба обчислити їх роботу. Як видно з одержаного виразу, це можна зробити лише тоді, коли сили незмінні або залежать тільки від положення (координат) точки, яка рухається, наприклад, сили ваги.

Теорему в диференціальній формі можна застосовувати при будь-яких діючих силах.