Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Робота сили та її вираз через криволінійний інтеграл

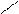Нехай тіло рухається прямолінійно і на всьому переміщенні 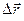на нього діє стала за величиною і напрямком сила 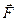, яка утворює кут 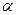з напрямком переміщення. Дію сили 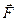на переміщенні 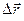, характеризують величиною, яку називають роботою.

Робота , яка виконана силою 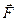, – це фізична величина, яка дорівнює ска­лярному добутку сили на переміщення:

,

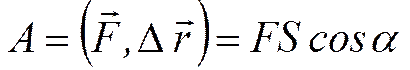де 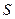– шлях пройдений тілом за час дії сили.

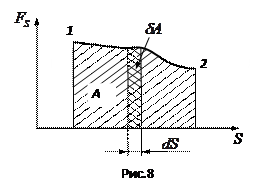
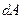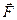Елементарною роботою сили на переміщенні 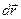називається скалярна величина

,

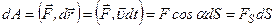де 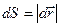- елементарний шлях, α – кут між векторами 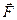і 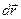, 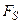- проекція вектора 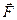на напрямок вектора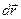

Якщо на тіло, яке рухається поступально, одночасно діють декілька сил, то робота рівнодійної сили при переміщенні на 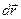дорівнює алгебраїчній сумі робіт складових сил:

.

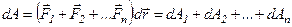Сила 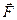, що діє на матеріальну точку або на тіло, яке рухається поступально, називається кон­сервативною або потенціальною, якщо робота 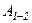, яка виконується цією силою при переміщенні точки (тіла) з одного довільного положення 1 в інше 2, не залежить від того, вздовж якої траєкторії відбулось це переміщення (рис. 9):

.

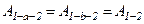Зміна напрямку руху вздовж траєкторії на протилежний спричинює зміну знака роботи (кут a замінюється на 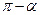і cos a змінює свій знак). Тому робота консервативної сили при переміщенні матеріальної точки вздовж замкненої траєкторії L (1-а-2-b-1) тотожно дорівнює нулю:

.

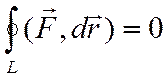Прикладами консервативних сил можуть бути сили тяжіння, гравітаційні сили, сили пружності, сили електростатич­ної взаємодії між зарядженими тілами.

Кінетичною енергією механічної системи називається енергія механічного руху цієї системи.

Сила 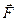, яка діє на тіло і викликає його рух, виконує роботу, а енергія рухомого тіла зростає на величину виконаної роботи:

.

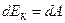Використовуючи скалярний запис другого закону Ньютона і помноживши обидві частини на елементарний шлях dS, отримаємо

.

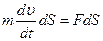Оскільки 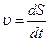, то

і

.

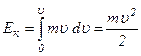співвідношення 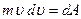вздовж деякої траєкторії від точки 1 до точки 2 в яких швидкість тіла 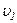і 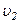відповідно:

.

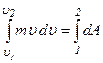Звідси,

.

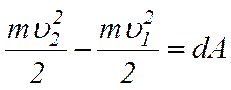Отже, зміна кінетичної енергії тіла дорівнює роботі, яка виконується над тілом.

Кінетичній енергії тіла можна надати і такого вигляду:

,

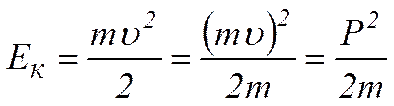де Р – імпульс тіла.

Кінетична енергія тіла не може бути від’ємною.

Повна кінетична енергія 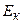системи дорівнює сумі кінетичних енергій 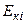всіх тіл, що входять до неї:

.

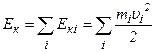Кінетична енергія системи залежить від величини мас і швидкостей руху тіл, що входять до неї. При цьому неістотно, як тіло з масою 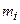набуло швидкості 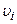. Цей висновок можна сформулювати так: кінетична енергія системи є функцією стану її руху.

Швидкість 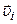істотно залежить від вибору системи відліку. В різних інерці­альних системах відліку, що рухаються одна відносно одної, швидкість 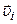і -го тіла системи, а отже, його кінетична енергія системи будуть неоднакові.

Кінетична енергія системи залежить від вибору системи відліку, тобто є величиною відносною.

Якщо в інерціальній системі відліку (і.с.в.) К кінетична енергія системи дорівнює 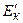, то в і.с.в. 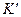, яка рухається відносно К поступально з швидкістю 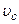, центра мас системи, то

,

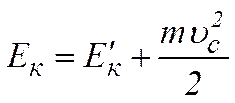де m – маса системи, 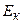- кінетична енергія системи відносно і.с.в. .

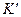Ця рівність описує теорему Кюніга: кінетична енергія механічної системи дорів­нює сумі кінетичної енергії цієї системи при її русі відносно і.с.в. 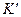, яка пос­тупально рухається з початком в центрі мас і кінетичної енергії, яку мала би матеріальна точка, що має масу, яка дорівнює масі всієї системи і рухається зі
швидкістю її центра мас.