
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построение векторных диаграмм
|
|
Гармоническое колебание изображается в виде вращающегося вектора амплитуды со скоростью ω:
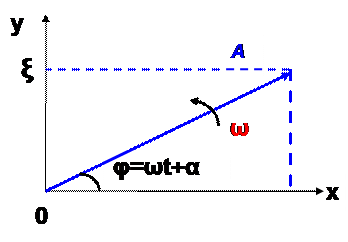
4.
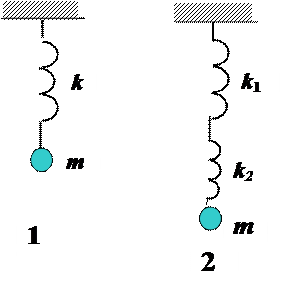 Период первого маятника Т, период второго:
Период первого маятника Т, период второго:
(k 1 = k 2 = k)
Варианты ответов
1) √ 0, 5 Т; 2) √ 2 Т; 3) 4 Т; 4) 2 Т; 5) Т/4
Р е ш е н и е
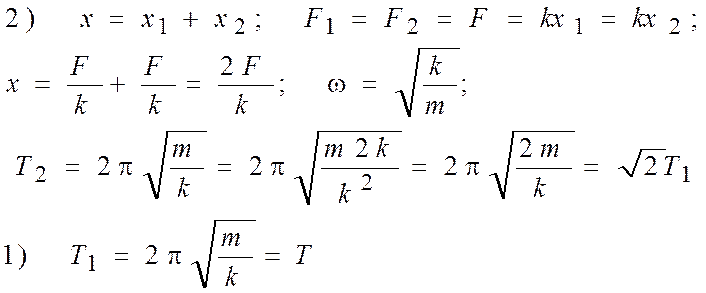
5. Складываются два гармонических колебания одного направления с одинаковыми периодами Т1 = Т2 = Т и равными амплитудами А1 = А2 = А0. При разности фаз Δ φ = 3π /2 амплитуда результирующего колебания равна … 1) А0√ 2; 2) 2А0; 3) 0; 4) 5/2А0.
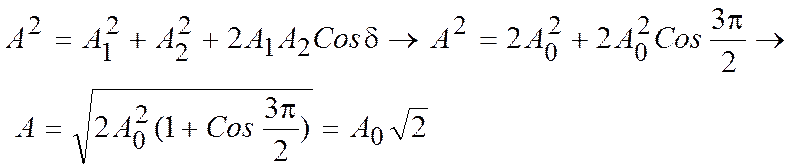
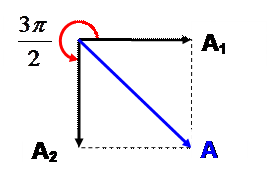 2-й способ решения более простой, применяя метод векторных диаграмм, откуда видно: А = √ 2А02 = А0√ 2;
2-й способ решения более простой, применяя метод векторных диаграмм, откуда видно: А = √ 2А02 = А0√ 2;
6. М.т. совершает гармоническое колебание по закону 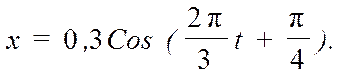 Максимальное значение скорости равно …
Максимальное значение скорости равно …
1) 0, 2π м/с; 2) π м/с; 3) 0, 1π м/с; 4) 2π м/с.
7. Складываются два гармонических колебания одинакового направления с одинаковыми периодами. Результирующее колебание имеет максимальную амплитуду при разности фаз, равной… 1) 0; 2) π; 3) π /4; 4) π /2
8. Складываются два гармонических колебания одинакового направления с одинаковыми частотами и равными амплитудами А0. При разности фаз ∆ φ = π амплитуда результирующего колебания равна… 1) 0; 2) А0√ 2; 3) 2А0; 4) А0√ 3
9. Складываются три гармонических колебания одного направления с одинаковыми периодами. Амплитуды и начальные фазы колебаний равны: 1) А 1 = 3 см, φ 1 = 0;
2) А2 = 2 см, φ 2 = π /2; 3) А3 = 2 см, φ 3 = π. Амплитуда и фаза результирующего колебания соответственно равны:
1) 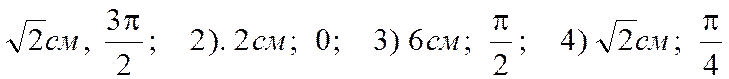
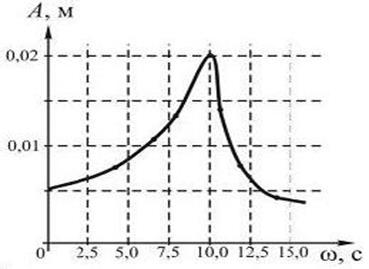
 10. На рис. представлена зависимость амплитуды вынужденных колебаний груза на пружине с жесткостью
10. На рис. представлена зависимость амплитуды вынужденных колебаний груза на пружине с жесткостью
k =10 H/м от частоты внешней силы. При малом затухании максимальная энергия в этой системе равна…
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
1) 0, 002 Дж; 2) 0, 004 Дж; 3) 20 Дж; 4) 40 Дж.
Резонанс → 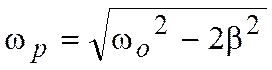 .
.
Т.к. β =0, то ω р = 10 с = ω о = 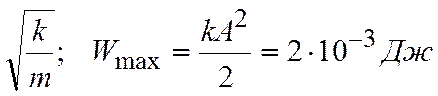
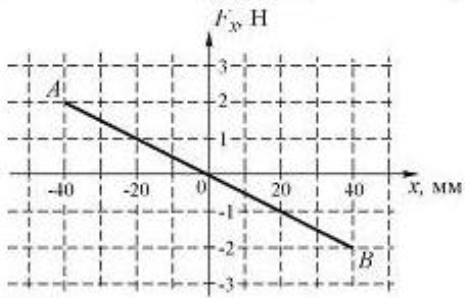 |
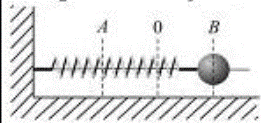 11. Шарик, прикрепленный к пружине и насаженный на горизонтальную направляющую, совершает гармонические колебания. На графике представлена зависимость проекции упругости пружины на положительное направление оси X от координаты шарика. Работа силы упругости при смещении шарика из положения А в положение В составляет … 1) 0Дж; 2) 4∙ 10-2 Дж;
11. Шарик, прикрепленный к пружине и насаженный на горизонтальную направляющую, совершает гармонические колебания. На графике представлена зависимость проекции упругости пружины на положительное направление оси X от координаты шарика. Работа силы упругости при смещении шарика из положения А в положение В составляет … 1) 0Дж; 2) 4∙ 10-2 Дж;
3) -4∙ 10-2 Дж; 4) 8∙ 10-2 Дж
Р е ш е н и е
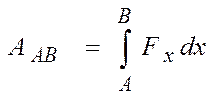 - геометрический смысл интеграла = площади S → AAO - AOB = 0.
- геометрический смысл интеграла = площади S → AAO - AOB = 0.
12. Точка М одновременно колеблется по гармоническому закону вдоль осей координат ОХ м ОУ с различными амплитудами, но одинаковой частоты. При разности фаз π /2 траектория точки М имеет вид:
 |
Варианты ответов: 1; 2; 3; 4.
Р е ш е н и е
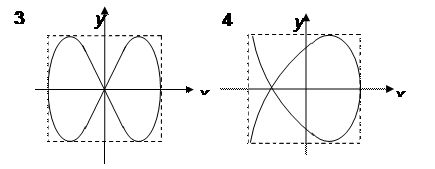
1) Разность фаз δ = ± π /2 → 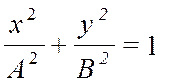 (7) – уравнение эллипса, приведенного к осям х и у, 2) δ = 0 → (4) →
(7) – уравнение эллипса, приведенного к осям х и у, 2) δ = 0 → (4) → 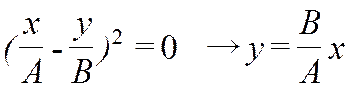 (5)- уравнение прямой (Рис. 2). Результирующее колебание является гармоническим вдоль этой прямой с частотой ω и амплитудой: А РЕЗ = √ А2 + В2.
(5)- уравнение прямой (Рис. 2). Результирующее колебание является гармоническим вдоль этой прямой с частотой ω и амплитудой: А РЕЗ = √ А2 + В2.
3) и 4): ω 1 ≠ ω 2 – частоты взаимно перпендикулярных колебаний неодинаковы.
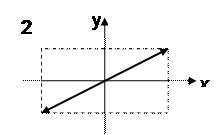
Траектория результирующего движения имеет вид довольно сложных кривых, называемых фигурамиЛиссажу.
На Рис. 3 показана одна из простейших траекторий, получающаяся при отношении ω 1: ω 2=1: 2 и δ = π /2.
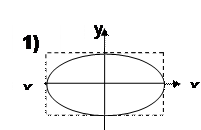
На Рис. 4 уравнения колебаний: 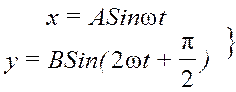 → ω 1: ω 2=3: 2 и δ = π /2.
→ ω 1: ω 2=3: 2 и δ = π /2.
|
|
