Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Формула Тейлора

Сначала рассмотрим функцию двух переменных 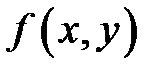. Предполагаем, что в некоторой окрестности точки 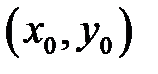существуют все частные производные функции 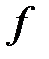до 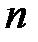-го порядка включительно. Фиксируем 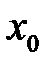, 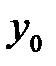. Запишем 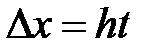, , 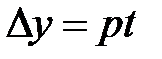тогда значение функции в точке 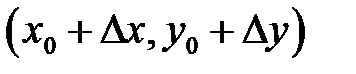запишется как 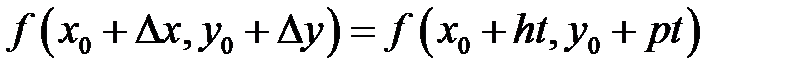. Фиксируем 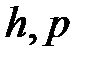и будем считать, что меняется только 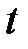, тогда

.

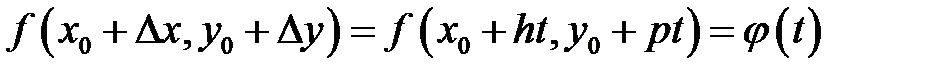Применим к функции 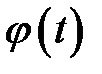формулу Маклорена с остаточным членом в форму Пеано:

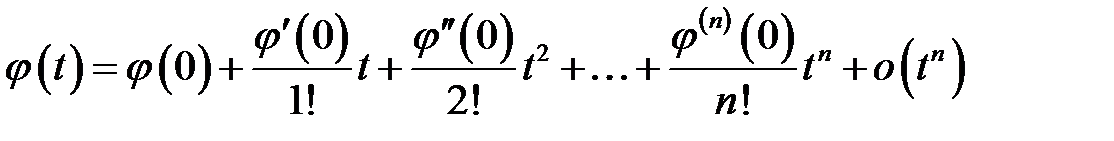
В соответствии с нашими обозначениями 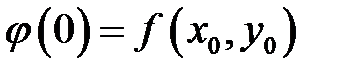. Вычислим производные функции 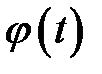через производные функции :

,

,

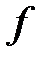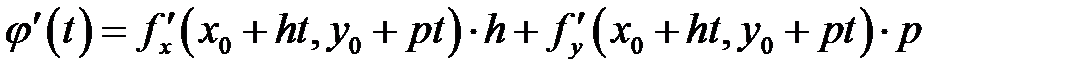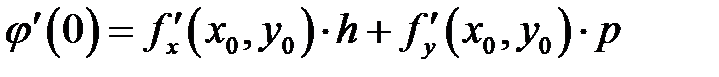аналогично

,

,

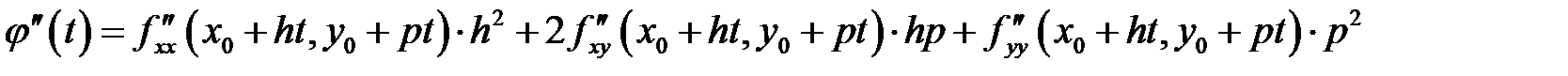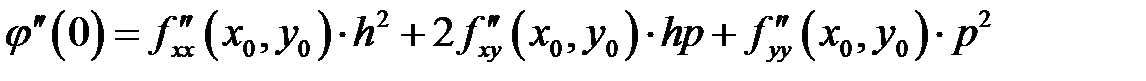Легко проверить, что 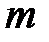-я производная имеет вид

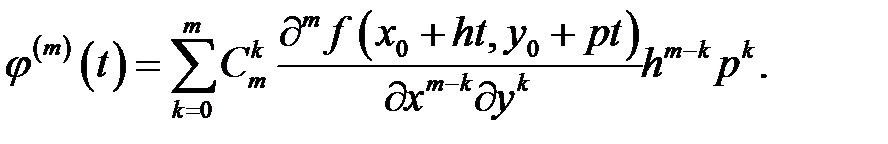
Подставив все это в формулу Маклорена для 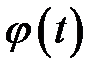и вернувшись к обозначениям 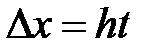, , 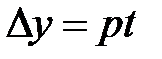мы получим

.

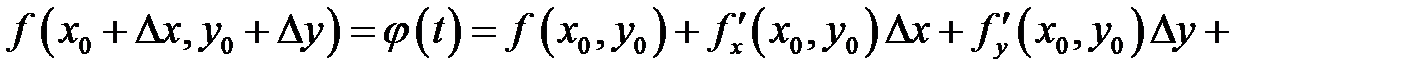
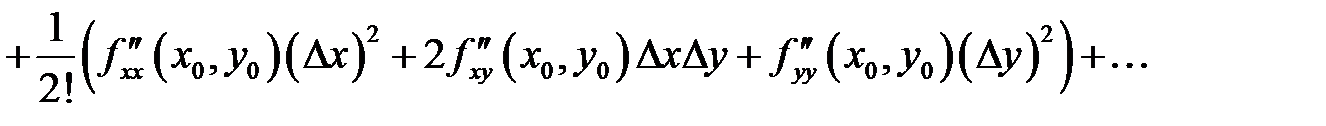
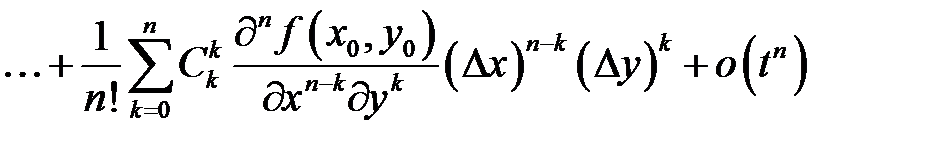Обозначим теперь , ,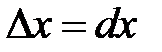

.

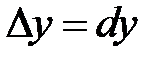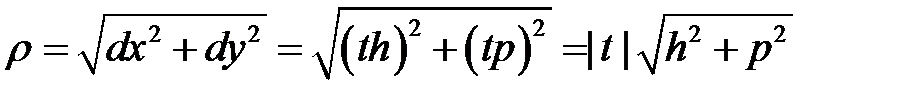Так как 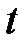и 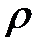отличаются постоянным множителем, то 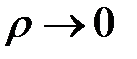при 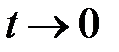и наоборот, а также 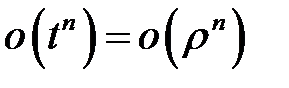(при 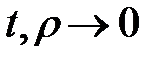). Тогда полученная нами формула Тейлора для функции двух переменных может быть записана в следующем виде:

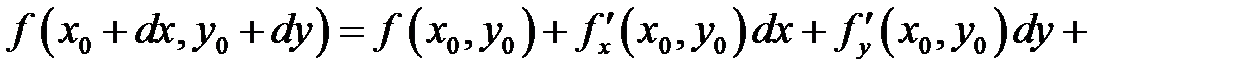
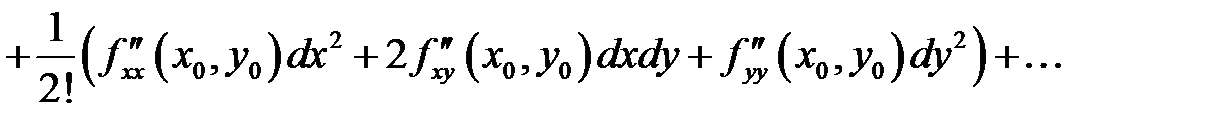
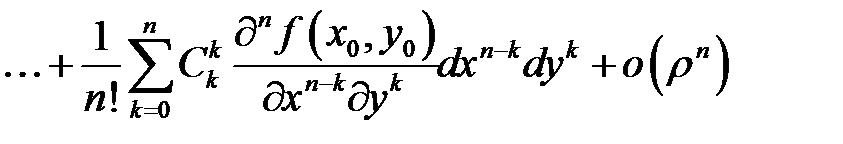
или

,

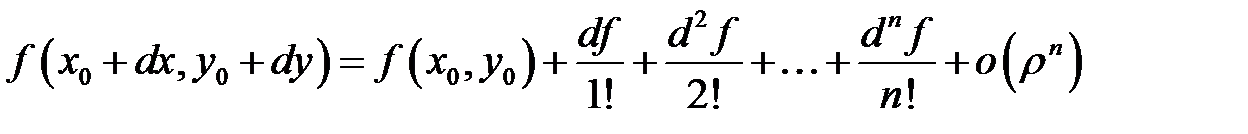где все дифференциалы берутся в точке 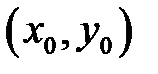.