
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Опорный меридиан и ортодромический курс. Преобразование курсов.
|
|
Ось гироскопа в начале полета может быть выставлена по абсолютно любому направлению. Пилоты привыкли, что курс 0° – это на север, 90° – на восток и т.д. Поэтому, чтобы численные значения гироскопического курса хотя бы примерно соответствовали сторонам света, сложилась практика выбирать не произвольное направление начала отсчета, а такое, чтобы оно совпадало с северным направлением истинного или магнитного меридиана какой-либо точки на маршруте – аэродрома вылета или посадки, ППМ и т.д. Такое направление, выбранное для начала отсчета курса (а значит и путевых углов, пеленгов и т.п.) называют северным направлением опорного меридиана, а измеренный от него курс получил название ортодромического курса (grid heading).
Таким образом, северное направление опорного меридиана – это в принципе произвольное направление, выбранное пилотом в качестве начала отсчета курса, и которое сохраняет ось идеального гироскопа. Если выставить ось гироскопа по этому направлению, то ортодромический курс и гироскопический курс – одно и то же. А если гироскоп еще не выставлен или по каким-то причинам ушел от заданного направления, то на шкале компаса одно значение (гироскопический курс, то есть курс, отсчитанный от оси гироскопа), а на самом деле по отношению к выбранному направлению опорного меридиана продольная ось ВС направлена под другим углом (ортодромический курс). Так же и с часами. Время, которое Вы хотите использовать (например, московское) соответствует ортодромическому курсу. А время, которое показывают Ваши часы (они еще может быть не выставлены или просто неточны) – соответствует гироскопическому курсу.
Таким образом, физически направление опорного меридиана – это направление оси гироскопа, который выставлен по выбранному направлению.
Но на практике опорным меридианом называют и земной меридиан, с которым это направление совпадает. Например, если ось гироскопа в начале полета выставлена по направлению магнитного меридиана аэродрома Пулково, то говорят, что опорным меридианом является магнитный меридиан Пулково. И в полете в районе Новосибирска считают, что гирополукомпас измеряет курс от пулковского магнитного меридиана.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Следует осознавать условность подобных выражений. Разумеется, сам гироскоп знать не знает, где это Пулково, и не может измерить от него курс. Он просто ведет себя так, как положено по законам физики. Данное выражение просто означает, что если вместе с гироскопом самолет переместится по ортодромии (именно по ортодромии!) в Пулково, то там направление этой оси совпадет с магнитным меридианом этого аэродрома.
Может ли ось гироскопа быть выставлена одновременно по двум или трем опорным меридианам? Конечно. Ведь под опорным меридианом на Земле понимается истинный или магнитный меридиан какой-то точки на маршруте, с которым совпадет ось гироскопа, если переместится в эту точку. Допустим, гироскоп выставлен по истинному меридиану Пулково. Но в полете меняются направления истинных меридианов из-за угла их схождения и магнитных меридианов из-за изменения магнитного склонения. Вполне может оказаться, что в какой-то точке маршрута ось гироскопа совпала с магнитным меридианом. Тогда его тоже можно считать опорным (рис. 5.26).
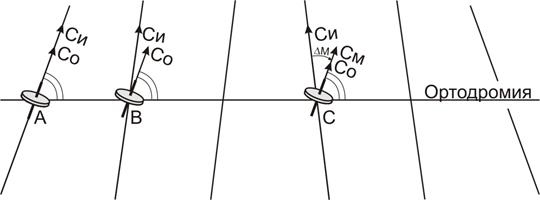
Рис. 5.26. Опорные меридианы
Преобразование курсов. Рассмотрим преобразование курсов на примере.
Допустим, что на аэродроме вылета ось гироскопа была выставлена по магнитному меридиану аэродрома с координатами
λ 0=78° в.д. φ 0=52° с.ш. Магнитное склонение на аэродроме вылета Δ M0=− 4°.
В настоящий момент ВС находится в точке с координатами места самолета
λ =86° в.д. φ =48° с.ш Магнитное склонение в точке нахождения ВС Δ M= − 1°.
Магнитный курс в данный момент γ м= 137 °. Требуется определить ортодромический курс γ 0, то есть курс относительно опорного меридиана.
В соответствии с правилом учета поправок для получения ортодромического курса к магнитному курсу нужно прибавить (переход в сторону «истинных» величин) магнитное склонение и азимутальную поправку:
γ 0 = γ м + Δ M + Δ А.
Магнитное склонение уже известно (Δ M=− 1°), а азимутальную поправку нужно рассчитать. Поскольку опорный меридиан магнитный, используем формулу (5.3):
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Δ А =(λ 0− λ) sin φ ср − Δ M0 = (78− 86) sin 50° –(− 4) = (− 8) 0, 76 +4= − 6+4=− 2°.
В приведенном расчете 50 ° – это среднее значение двух широт (48 ° и 52 °). На практике при его определении нет необходимости рассчитывать это значение точно (учитывать доли градуса), поскольку отсчитать курс с компаса можно в лучшем случае с точностью до градуса. По этой же причине угол схождения меридианов в этой формуле, более точное значение которого (− 6, 13 °), округлен до целого значения градусов (− 6 °).
Тогда:
γ 0 = γ м + Δ M + Δ А = 137 + (− 1)+ (− 2)= 137 − 1 − 2=137 − 3=134 °.
Заметим, что величина (− 3 °), которая была прибавлена к магнитному курсу для получения ортодромического, это и есть условное магнитное склонение.
Таким образом, пользуясь правилом учета поправок и формулами (5.2, 5.3) для расчета азимутальной поправки, можно выполнить любые преобразования курсов, а также пеленгов, путевых углов и любых направлений.
Мнемоническая схема преобразования курсов.
Такая схема (рис. 5.31) позволяет «перейти» от меридиана одной точки (истинного или магнитного) к меридиану другой (тоже истинному или магнитному).
Две вертикальные линии (см. рис. 5.31) условно изображают меридианы, от одного из них курс известен, а от другого нужно узнать. На каждом из них кружки с буквами И и М, что означает истинный и магнитный. На каждом из меридианов истинный и магнитный курсы отличаются на магнитное склонение Δ М, на каждом из меридианов оно свое.
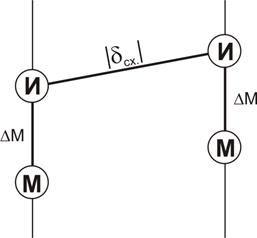
Рис. 5.31. Мнемоническая схема преобразования направлений
Верхние кружки с надписями И соединены наклонной линией, на которой надписано |δ сх| (угол схождения меридианов по абсолютной величине). Важно обратить внимание на то, что эта наклонная линия идет вверх, если смотреть слева направо (с запада к востоку). То есть, кружки на правом меридиане выше, чем на левом.
Перед использованием мнемонической схемы целесообразно вначале рассчитать угол схождения меридианов по модулю, то есть, не обращая внимания на его знак. Знак будет учтен «автоматически» при использовании схемы.
Для определения модуля угла схождения меридианов нужно просто посмотреть, на сколько градусов различаются долготы двух меридианов и умножить это число на синус средней широты. Этот расчет удобно выполнить на НЛ-10, причем обычно высокая точность расчета не требуется, если курс достаточно рассчитать с точностью до градуса.
Всегда от одного из меридианов курс известен, а от другого его нужно узнать. Сначала необходимо определить, какая из двух вертикальных линий на схеме будет изображать тот и другой меридиан. Сделать это нетрудно, зная долготы меридианов, если вспомнить, что долгота возрастает к востоку (на рисунке – вправо).
Тот курс, который задан, может отсчитываться от истинного или магнитного меридиана. В соответствии с этим «движение» по схеме начинается с кружка И или М на том из двух меридианов, от которого известен курс.
Закончить «движение» нужно на меридиане второй точки, на кружке И или М в зависимости от того, какой именно курс нужно определить.
Смысл применения этой схемы очень прост. Перемещаясь по ней от исходного кружка к конечному, нужно прибавлять (вычитать) все те поправки (со своим знаком), которые встретятся на пути. Причем, при движении вверх – прибавлять, а при движении вниз – вычитать.
Рассмотрим применение этой схемы на том же примере, для которого расчет был проведен по формулам.
Напомним исходные данные.
Опорный меридиан – магнитный, λ 0=78° в.д., φ 0=52° с.ш. Магнитное склонение на опорном меридиане Δ M0=− 4°.
В настоящий момент ВС находится в точке с координатами λ =86° в.д., φ =48° с.ш, м агнитное склонение в точке нахождения ВС Δ M= − 1°.
Магнитный курс в данный момент γ м= 137 °.
Требуется определить ортодромический курс.
Разность долгот двух меридианов (86 − 78)=8 (считаем по модулю, не обращая внимания на знак). Умножив на синус средней широты 50°, получим с точностью до градуса 6° (модуль угла схождения меридианов).
Долгота места самолета больше (восточнее), чем долгота опорного меридиана, следовательно, на схеме меридиан самолета справа, а опорный слева.
По условию задачи известен магнитный курс, следовательно, расчет начнем с кружка М на правом меридиане схемы (ведь магнитный курс измеряется от меридиана места самолета, который в данном случае на схеме справа).
Найти требуется ортодромический курс, то есть курс от опорного меридиана (на схеме он слева), причем опорный меридиан является по условию задачи магнитным. Значит, перейти по схеме нужно к кружку М на левом меридиане.
Начиная от заданного курса (137º) перемещаемся на правом меридиане вверх, следовательно, нужно прибавить магнитное склонение, которое имеет место на данном меридиане (− 1):
137+(− 1)=136.
Далее, от правого кружка И переходим к левому кружку И. Поскольку движение идет вниз, вычитаем соответствующую поправку (6):
136− 6=130.
И, наконец, уже на левом (в данном случае, опорном) меридиане нужно спуститься вниз к кружку М, следовательно, вычесть магнитное склонение на этом опорном меридиане:
130− (− 4)=134°.
Это и будет ортодромический курс от опорного меридиана.
Разумеется, ответ совпал с тем, который был получен по формулам.
Естественно, при решении других задач такого типа может понадобиться переходить не от правого меридиана к левому, а наоборот. Или начинать и заканчивать переход от других кружков на схеме.
При использовании данной схемы важно правильно понимать, что решение задачи зависит не от того, куда летит самолет, то есть движется он на восток или на запад. Играет роль только то, от какого меридиана к какому осуществляется переход – от более восточного к более западному или наоборот. Куда движется ВС неважно, может, оно просто стоит на стоянке.
Действительно, в приведенном примере был магнитный курс 137° (самолет летит на юго-восток), и при пересчете в ортодромический он уменьшился на 3° и стал равным 134°. Но если бы изначально магнитный курс в условии задачи был, например, 270° (ВС летит на запад), он тоже при пересчете уменьшился бы на 3° и ортодромический курс составил бы 267°: ведь исходный и конечный меридианы те же самые. А куда направлена продольная ось самолета не имеет значения.
Если данную схему мысленно держать перед глазами и правильно применять, то после тренировки можно быстро и безошибочно решать подобного рода задачи без запоминания формул.
|
|
