
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!
Ортодромичность курсового гироскопа
|
|
Теперь после анализа поведения курсового гироскопа на неподвижном самолете рассмотрим, как он будет вести себя в случае, когда ВС перемещается по ортодромической линии пути. Общий случай – полет по произвольной траектории, будет рассмотрен далее.
Широкое применение гироскопических курсовых приборов в навигации основывается на том, что курсовой гироскоп обладает ортодромичностью.
Свойство ортодромичности гироскопа заключается в том, что при полете по ортодромии ось гироскопа сохраняет с этой ортодромией постоянный угол. Разумеется, речь идет о курсовом гироскопе, снабженном механизмами горизонтальной и азимутальной коррекции и не имеющем инструментальных погрешностей, вызванных его неточным изготовлением, износом и т.д. Можно сказать, что речь идет об идеальном гироскопе, который ведет себя точно так, как ему положено себя вести в соответствии с законами физики. Конечно, идеальных гироскопов в природе не существует, а реальные гироскопы имеют ряд погрешностей, но они будут рассмотрены позже.
Свойство ортодромичности означает, что если перед началом полета установить ось гироскопа в каком-либо направлении и выполнять полет точно по ортодромии, то угол между осью гироскопа и ортодромией будет сохраняться (рис. 5.24).
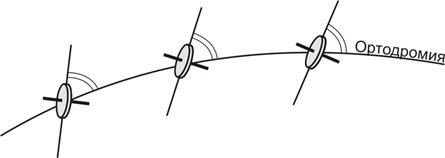
Рис. 5.24. Ортодромичность курсового гироскопа
Свойство ортодромичности не является каким-то дополнительным специфическим свойством, обнаружившимся у курсовых гироскопов. Оно является следствием основного свойства любого вращающегося тела сохранять направление оси своего вращения. Конечно, с учетом того, что механизм горизонтальной коррекции непрерывно удерживает ось гироскопа в текущей горизонтальной плоскости.
Свойство ортодромичности имеет математическое доказательство: можно показать, что скорость вращения оси гироскопа вокруг вертикальной оси, вызванная перемещением самолета, оказывается равной скорости изменения путевого угла ортодромии при полете по ней ВС. Получается, что с какой скоростью поворачивается ось гироскопа, с такой же скоростью и в ту же сторону «поворачивает» сама ортодромия относительно текущего меридиана. А угол между ними при этом остается постоянным.
Убедиться в наличии у гироскопа свойства ортодромичности можно и мысленно без всяких формул на основе следующих рассуждений.
Будем считать, что гирополукомпас снабжен механизмом азимутальной коррекции, который компенсирует уход гироскопа, вызванный вращением Земли. Поскольку этот уход компенсирован, то Землю можно считать неподвижной, не учитывать ее вращение.
Также предположим, что ветра нет и, следовательно, угол сноса равен нулю. В этом случае продольная ось ВС в полете также все время направлена по ортодромии. Такое допущение никак не повлияет на правильность выводов.
Для начала рассмотрим частный случай, когда ось гироскопа ориентирована прямо в направлении ортодромии, по которой выполняется полет.
Напомним, что ортодромия – это большой круг на земной сфере. Ее плоскость проходит через центр этой сферы и, следовательно, касательная к ортодромии, перепендикулярная ее радиусу, лежит в горизонтальной плоскости (рис.5.25).
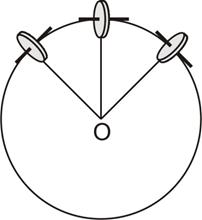
Рис. 5.25. К объяснению ортодромичности гироскопа
В полете ось гироскопа стремится сохранять свое направление в инерциальной системе отсчета, например, на какую-то звезду, на которую она вначале оказалась направлена. Если бы в гирополукомпасе отсутствовал механизм горизонтальной коррекции, то при перемещении ВС в другую точку ортодромии ось гироскопа сохраняла бы свое направление на звезду, но отклонилась бы от текущей горизонтальной плоскости, поскольку эта плоскость изменила свое положение. Но механизм горизонтальной коррекции непрерывно принудительно удерживает ось гироскопа горизонтально (см. рис.5.25). Таким образом, ось гироскопа меняет свое положение, но ее наклон происходит в плоскости самой ортодромии. Вправо или влево никакого отклонения нет, и ось гироскопа все время направлена вдоль ортодромической линии пути.
Таким образом, для данного частного случая свойство ортодромичности гироскопа вполне очевидно – он действительно сохраняет постоянный (в данном случае – нулевой) угол с ортодромией.
Теперь представим себе, что на ВС в одной и той же точке (условно, конечно) находятся одновременно два гироскопа. Ось первого, как и в предыдущем случае, направлена по ортодромии, а второго – под некоторым углом к ортодромии и, следовательно, к оси первого гироскопа. Благодаря механизму горизонтальной коррекции обе оси гироскопов расположены горизонтально.
При перемещении ВС ось первого гироскопа, как мы уже выяснили, будет все время направлена по ортодромии. А как будет вести себя второй гироскоп?
Оба гироскопа совершенно равноправны и стремятся сохранить свои направления в пространстве (каждый на свою звезду). Но механизм горизонтальной коррекции по мере перемещения ВС разворачивает их оси так, чтобы они оставались в текущей горизонтальной плоскости, общей для обоих гироскопов. Этот разворот происходит в вертикальной плоскости, то есть один конец оси гироскопа опускается, другой – поднимается. Но никакого бокового поворота (вправо-влево) не происходит, поэтому угол между осями гироскопов сохраняется тем же, каким он был вначале. А поскольку ось первого гироскопа направлена по ортодромии, то значит и ось второго гироскопа сохраняет с ортодромией на протяжении полета постоянный угол. В этом и заключается свойство ортодромичности.
Таким образом, в полете по ортодромии при отсутствии ветра, когда продольная ось ВС направлена по этой ортодромии, сохраняется постоянным угол между осью гироскопа и продольной осью ВС. Но этот угол – это гироскопический курс. Следовательно, при полете по ортодромии гироскопический курс сохраняется постоянным. Но тогда справедливо и обратное утверждение: для полета по ортодромии необходимо выдерживать постоянный гироскопический курс. Этим и объясняется важность гироскопических курсовых приборов для навигации. Ведь ЛЗП имеет форму ортодромиии и значит полет по ней можно легко осуществить, если лететь с постоянным гироскопическим курсом.
Это утверждение остается справедливым и при наличии ветра. Просто будет иметь место угол сноса и для полета по заданной ортодромической ЛЗП нужно выдерживать гироскопический курс, отличающийся от направления ортодромии на величину этого угла сноса. Продольная ось ВС уже не будет направлена по ортодромии, но гироскопический курс все равно будет постоянным, отличающимся от штилевого на угол сноса.
|
|
