Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Потоки заявок

Заявки – вимоги на обслуговування.

Потік заявок – це послідовність подій, що відбуваються одне за іншим у якісь моменти часу. Це потік викликів на тех. станцію, потік рекомендованих листів на поштовій відділення, потік збоїв ЕОМ, потік пострілів по меті й т.д.

Розрізняють потік однорідних подій (заявок) – якщо вони (заявки) розрізняються тільки моментами появи, і, відповідно, потік неоднорідних подій. З іншої сторони існують одномірні й багатомірні потоки.

Одномірний потік – це потік, заявки якого не відрізняються друг від друга.

Багатомірний потік – це потік, заявки якого мають друг перед іншому пріоритети, наприклад, або різні потреби в ресурсах ЕОМ (бувають завдання «короткі» і потребуючі багато часу для рішення) – теж наприклад.

Завдання може бути такий довгої, що заблокує всі ресурси, і лагідні будуть дуже довго чекати.

Ще один параметр поділу потоків: регулярні й випадкові.

У регулярному потоці події треба через строго певні проміжки часу (це й «періодичні» потоки - крайній випадок випадковості: -)

Коли час прибуття заявки випадково, проміжки часу між двома заявками випадкові – це випадкові потоки.

Найбільш популярний випадковий потік - найпростіший або стаціонарний пуассоновский. Назва «пуассоновский» пов'язане з тим, що число подій за час? буде розподілено за законом Пуассона.

Найпростіший потік грає серед потоків подій особливу роль (як нормальний закон серед інших законів розподілу – як сума великого числі незалежних випадкових величин). При підсумовуванні випадкових потоків виходить потік, близький до найпростішого. Імовірність того, що за час t відбудеться рівно m подій 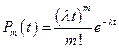- це закон розподілу Пуассона.

a=λ t – це середнє кількості заявок на проміжку t (скільки заявок укладеться в цьому проміжку).

λ – це щільність потоку (середнє число подій, що доводиться на одиницю часу).

Пуассоновский потік має наступні властивості:

1) Стаціонарність – коли ймовірність влучення певного числа подій на ділянку часу t залежить тільки від довжини ділянки й не залежить від того, де саме на осі 0t розташована ця ділянка. Т.е. стаціонарність позначає сталість щільності потоку.

Приклад: На тех. станцію в денний час надходить однакове число заявок в одиницю часу. А ввечері різке зростання числа вимог. Тоді на цих сусідніх ділянках потік не буде стаціонарним.

2) Безпіслядії – коли для будь-яких не ділянок, що перекриваються, часу число подій, що попадають на один з них не залежить від числа подій, що попадають на інші.

Т.е. надходження заявок не залежить друг від друга, коли моменти викликів не залежать від моментів, які будуть потім.

3) Ординарність – коли ймовірність влучення на елементарну ділянку Δ t двох або більше подій пренебрежимо мала в порівнянні з імовірністю влучення першої події.

Тобто. заявки надходять «по одинаку».