Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Понятия собственного значения и собственного вектора матрицы

Лекция 22. Введение в проблему собственных значений

План

Понятия собственного значения и собственного вектора матрицы

Задачи, приводящие к вычислению собственных значений

Подобное преобразование матрицы, его свойства

Свойства собственных значений и собственных векторов матрицы. Теорема о спектральном разложении матрицы

Связь между спектральным радиусом и матричной нормой

Понятия собственного значения и собственного вектора матрицы

Определение 1. Скаляр называется собственным значнием, а вектор 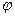собственным вектором матрицы , если выполняется равенство:

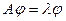. (1)

При этом пара 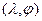называется собственной парой матрицы .

Таким образом, собственный вектор – это такой специальный вектор, который при умножении на матрицу не меняет своего направления (при ) или меняет на противоположное (при ).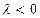

Каждому собственному значению матрицы соответствует бесконечно много собтвенных векторов. Действительно, если 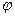- собственный вектор , отвечающий собственному значению 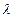(т.е. выполняется равенство (1)), то 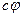, где 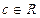, также собственный вектор , отвечающий собственному значению 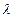. Действительно:

,

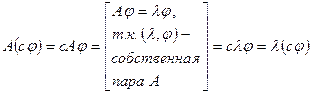т.е. по определению 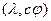- собственная пара матрицы при любом .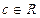

Определение 2. Многочлен

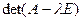
относительно скаляра 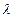называется характеристическим многочленом матрицы (здесь 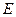- единичная матрица соответствующего размера), а уравнение

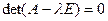
характеристическим уравнением.

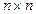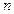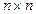Если матрица имеет размеры , то характеристический многочлен – это многочлен степени . Корни характеристического уравнения – это собственные значения матрицы , следовательно, -матрица имеет 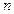однозначно определяемых собственных значения.

Определение 3. Множество всех собственных значений матрицы называется ее спектром.