Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Тройной интеграл в декартовых координатах. Свойства. Оценка. Теорема о среднем.

Предположим, что область интегрирования 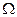в тройном интеграле 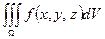ограничена гладкими поверхностями, заданными в прямоугольной декартовой системе координат 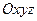. Разобьем область интегрирования на элементарные области 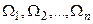плоскостями, параллельными координатным плоскостям, 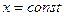, , 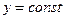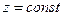. Тогда элементарный объем каждой области 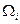будет равен .

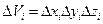По определению:

.

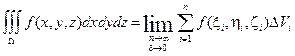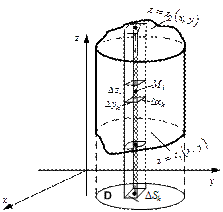
Рис. 1.

Пусть область 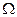однозначно проектируется в область 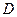на плоскости 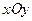. При этом поверхность, которая ограничивает область 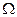, можно разбить на две поверхности: поверхность 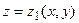, ограничивающая 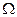снизу, и поверхность 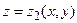, ограничивающая сверху (рис. 1).

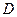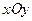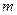Разобьём область на плоскости на элементарных областей 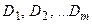. Обозначим через 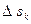площадь элементарной области .

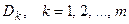На каждой элементарной области построим цилиндр с образующей, параллельной оси 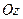. Такой цилиндр вырежет на граничных поверхностях 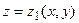и 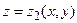некоторые элементарные области, которые будем считать плоскими и параллельными координатной плоскости 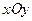. Каждый цилиндр разобьем на 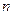частей плоскостями, параллельными координатной плоскости 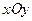, и расстояния между плоскостями обозначим через .

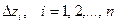В результате область 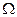разобьётся на элементарные цилиндры 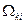с площадью основания 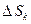и высотой 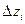. Объём элементарного цилиндра равен: .

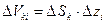В каждом элементарном цилиндре 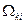выберем точку 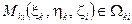. Тогда интегральная сумма примет вид:

,

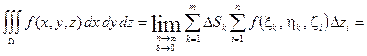
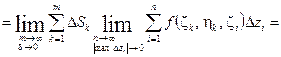
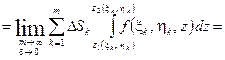
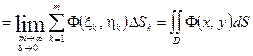где функция 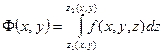является интегралом с переменным верхним и нижним пределом.

Следовательно, тройной интеграл равен двойному интегралу по проекции на плоскость 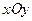области 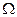. Подынтегральной функцией этого двойного интеграла является интеграл по переменной 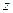от функции 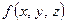в пределах: от значения 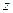на поверхности, являющейся нижней границей области 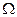, до значения 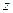на поверхности, являющейся верхней границей .

.

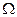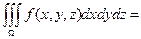
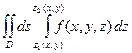Задача

Вычислить объем тела, ограниченного поверхностями , ,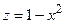

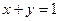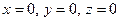
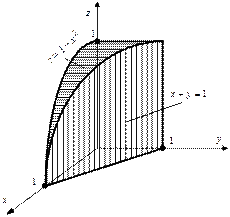
Рис. 2.