Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Дифференцирование сложной ФНП. Производные неявных функций.

Функции нескольких переменных. Предел последовательности. Предел функции нескольких переменных. Непрерывность ФНП.

Если каждой паре (x, y) значений двух независимых друг от друга, переменных величин x и y, из некоторой области их изменения D, соответствует определенное значение величины z, то говорят, что z функция двух независимых переменных x и y, определенная в области D.

В математике пределом последовательности называют объект, к которому члены последовательности стремятся или приближаются с ростом номера.

Для функции нескольких переменных можно определить понятие предела только по одной из переменных. Из этого возникает понятие повторного предела. В зависимости от последовательности взятия пределов будут различные повторные пределы.

Число А называется пределом функции F(M), где M(x1, x2, x3,..., xn)-точка n-мерного пространства, при стремлении точки М к точке М0(x10, x20,..., xn0) любым образом, если для всякого сколь угодно малого e> 0 существует такое число d> 0 (d-эпсилон), что из условия |MM0|< d, где |MM0|-расстояние между точками М и М0, следует |F(x1, x2,..xn)-A|< d.

Частное и полное приращения функции нескольких переменных. Частные производные и частные дифференциалы.

Пусть задана функция z = f(х, у). Так как х и у – независимые переменные, то одна из них может изменяться, а другая сохранять постоянное значение. Дадим переменной х приращение ∆ х, сохраняя значение переменной у неизменным. Тогда функция z получит приращение, которое назовем частным приращением z по х и обозначим

∆ х z: ∆ х z = f(x + ∆ x, y) – f(х, у).

Наконец, если аргументу х дать приращение ∆ х, а аргументу у – приращение ∆ у, то получим полное приращение функции z:

∆ z=f(x+∆ x, y+∆ у)–f(х, у).

Частная производная-производная по одной из переменных в функции нескольких переменных, только в ней все остальные переменные принимаются за константы, а потом находится производная. С дифференциалом то же самое, но только находится интеграл.

Дифференцируемость функции. Полный дифференциал.

Дифференци́ руемая (в точке) фу́ нкция — это функция, у которой существует дифференциал (в данной точке). Дифференцируемая на некотором множестве функция — это функция, дифференцируемая в каждой точке данного множества.

Главная часть приращения функции, линейная относительно приращения переменных, называется полным дифференциалом. dZ или df(x, y, z...)

Дифференцирование сложной ФНП. Производные неявных функций.

Теорема.Пусть u = f (х, у) задана в области D и пусть х = х(t) и у = у(t) определены в области 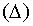, причём, когда 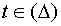, то х и у принадлежат области D. Пусть функция u дифференцируема в точке M0(x0, y0, z0), а функции х(t) и у(t) дифференцируемы в соответствующей точке t0, то сложная функция u = f [x(t), y(t)]=F (t) дифференцируема в точке t0 и имеет место равенство:

.

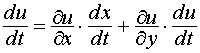Доказательство.Так как u дифференцируема по условию в точке (x0, y0), то её полное приращение представляется в виде

.

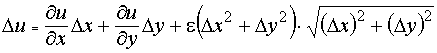Разделив это соотношение на 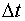, получим:

.

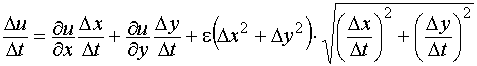Перейдём к пределу при и получим формулу

.

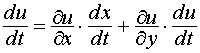Замечание 1.Если u = u(x, y) и x = x, y = y(x), то полная производная функции u по переменной х

или .

Последнее равенство можно использовать для доказательства правила дифференцирования функции одной переменной, заданной неявно в виде F(x, y) = 0, где y = y(x) (см. тему № 3 и пример 14).

Имеем: 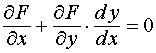. Отсюда 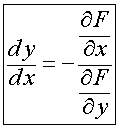. (6.1)

Вернёмся к примеру 14 темы № 3:

;

;

;

.

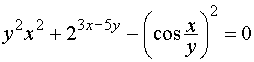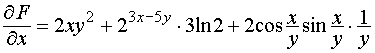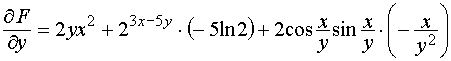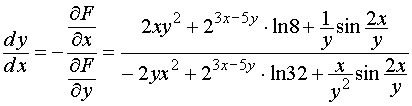Как видим, ответы совпали.

Задание. Найти вторую производную 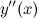неявной функции .

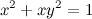Решение. Продифференцируем левую и правую часть заданного равенства, при этом помним, что 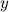является функцией переменной , поэтому производную от нее будем брать как производную от сложной функции. В итоге получаем:

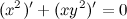
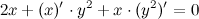
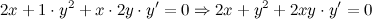
Из полученного равенства выражаем :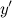

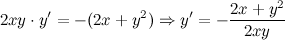
Для нахождения второй производной продифференцируем равенство 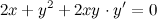еще раз:

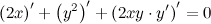
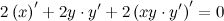
Подставив вместо 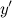найденное выше выражение, получаем:

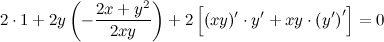
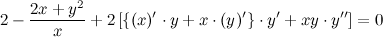
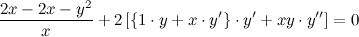
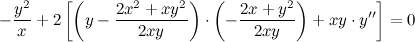
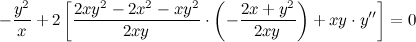
После упрощения получаем:

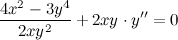
Из полученного равенства выражаем вторую производную :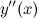

Ответ.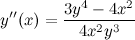