Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Экстремум функции двух переменных. Необходимые и достаточные условия существования экстремума.

Максимум и минимум функции называются экстремумами функции.

Теорема (достаточное условие экстремума функции двух переменных). Пусть в некоторой области, содержащей точку 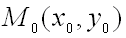функция 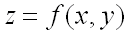имеет непрерывные частные производные до третьего порядка включительно. Пусть, кроме того, точка 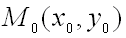является критической точкой функции 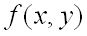, т.е.
,
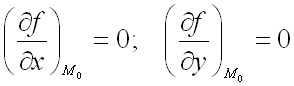тогда при :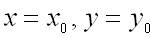
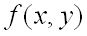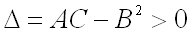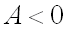1) имеет максимум, если дискриминант и , где ;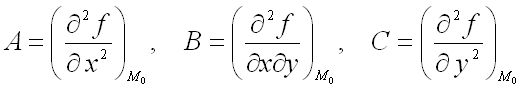
2) 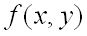имеет минимум, если дискриминант 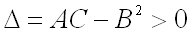и ;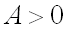
3) 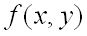не имеет ни минимума, ни максимума, если дискриминант ;
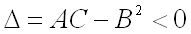4) если 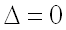, то экстремум может быть, а может и не быть (требуется дополнительное исследование).

Теорема (необходимое условие экстремума)

Если точка 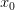— точка экстремума функции 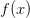, то она критическая.

Доказательство

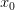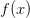
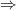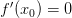
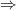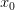По условию точка — точка экстремума функции по теореме Ферма производная точка является критической.

Теорема (первое достаточное условие экстремума в терминах первой производной)

Пусть функция 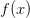определена и дифференцируема в некоторой окрестности точки 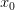, кроме, быть может, самой точки 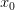и непрерывна в этой точке. Тогда:

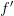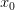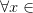
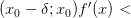
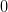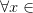
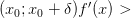
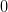Если производная меняет знак с «-» на «+» при переходе через точку : и , то 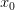— точка строго минимума функции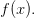

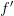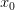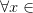
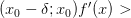
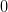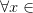
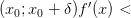
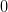Если производная меняет знак с «+» на «-» при переходе через точку : и , то 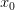— точка строго максимума функции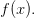