Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Пример 12.

а) 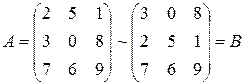. Здесь у матрицы A поменяли первую и вторую строку местами.

б) 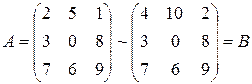. Здесь у матрицы A все элементы первой строки умножили на число 2.

в) 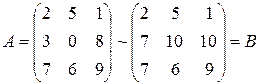. Здесь к элементам второй строки прибавили соответствующие элементы первой строки, умноженные на 2.

Определение 16. Матрица 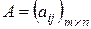называется матрицей треугольного вида, если все элементы, расположенные ниже элементов 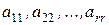, , 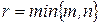в соответствующих столбцах, т.е. ниже главной диагонали, равны нулю.

Пример 13. Матрицы 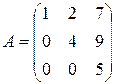, , 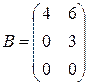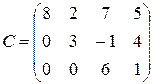- матрицы треугольного вида.

Замечание. Иногда треугольные матрицы рассмотренного вида называют правыми верхними треугольными матрицами. Соответственно, матрицы, у которых все элементы, расположенные выше элементов 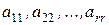, , 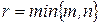в соответствующих столбцах (т.е. выше главной диагонали), равны нулю, называют левыми нижними треугольными матрицами (Шев. КР., стр. 118). Используя побочную диагональ 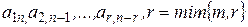, можно, соответственно, также ввести левую верхнюю и правую нижнюю треугольные матрицы.

Так как для изложения рассматриваемого нами курса достаточно использования треугольных матриц правого верхнего вида, далее во всех случаях мы их будем называть просто матрицами треугольного вида.

Теорема 3. Любая матрица с помощью элементарных преобразований может быть приведена к треугольному виду.

Доказательство. Проведите самостоятельно.

Справедливость данного утверждения легко подтвердить на следующем примере.