Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Пример 3. .

Замечание. Нетрудно заметить, что операции сложения матриц и умножения матрицы на число, обладают следующими свойствами:

1) 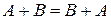- коммутативность,

2) 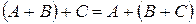- ассоциативность,

3) ,

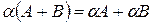4) ,

5) ,

здесь А, В и С – матрицы одного и того же размера, a и b - действительные или комплексные числа. Справедливость данных свойств следует из справедливости соответствующих свойств на множестве действительных и комплексных чисел, ведь рассматриваемые действия над матрицами сводятся к выполнению соответствующих операций над их элементами, которые являются числами.

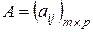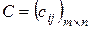Определение 7. Произведением матриц и называется матрица , элементы которой определяются по правилу:

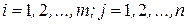, . (13)

Обозначение: или более кратко .

Нетрудно заметить, что каждый элемент матрицы-произведения С, стоящий на пересечении i -ой строки и j -го столбца, – представляет собой сумму произведений элементов i -ой строки матрицы А на соответствующие элементы j- го столбца матрицы В. На рисунке 1 представлено схематическое правило получения элемента .

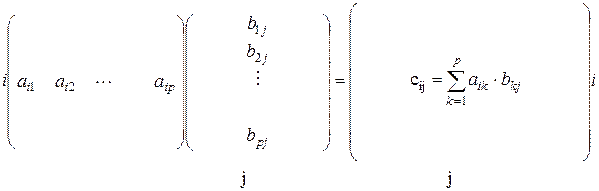
Рисунок 1 – Схематическое правило получения элементов

матрицы произведения

Из формулы (13) видно, что произведение матриц можно определить только в том случае, когда число столбцов первого сомножителя равно числу строк второго сомножителя.

На практике, при получении произведения матриц результирующую матрицу заполняют, как правило, по столбцам. Т.е. сначала определяют суммы произведений элементов строк первого сомножителя на соответствующие элементы первого столбца второго сомножителя, которые будут составлять первый столбец результирующей матрицы; затем находят суммы произведений элементов строк первого сомножителя на соответствующие элементы второго столбца второго сомножителя, которые будут составлять второй столбец результирующей матрицы, и так далее. Размеры матрицы-произведения зависят от числа строк первого сомножителя и числа столбцов второго сомножителя.

Пример 4. Если 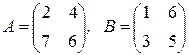, то определяется так:

.

Пример 5. Пусть 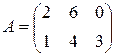, , 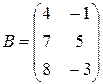тогда:

=

= ;

=

= .

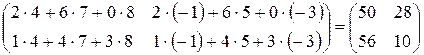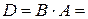
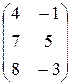
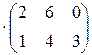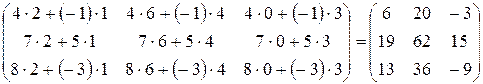Нетрудно заметить, что для рассмотренных в примере 5 матриц А и В, .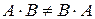

Замечание. Таким образом, операция умножения матриц в общем случае не является коммутативной (хотя существуют матрицы, для которых это свойство выполняется, о них мы поговорим ниже), свойства ассоциативности и дистрибутивности сохраняются:

1) ;

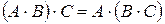2) 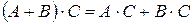и .

Справедливость этих свойств проверьте самостоятельно.

Определение 8. Матрицы А и В называются коммутативными (перестановочными), если .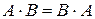

Очевидно, что коммутативными могут быть только квадратные матрицы одинакового размера.

Определение 9. Набор элементов 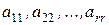матрицы 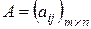, где 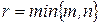, называется главной диагональю матрицы.

Пример 6. Для матрицы 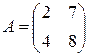главная диагональ – набор элементов .

Пример 7. Для матрицы 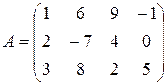главная диагональ – набор элементов .

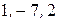Определение 10. Квадратная матрица 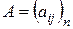называется диагональной, если все элементы матрицы, расположенные вне главной диагонали равны нулю, т.е. если .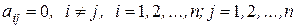