
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Пример 10. Матрицыи -единичные матрицы.
|
|
Теорема 2. Если 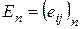 , где
, где 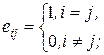 то для любой матрицы
то для любой матрицы 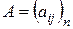
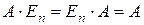 . (14)
. (14)
Доказательство.
Пусть матрица 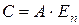 , тогда, согласно определению 7, матрица
, тогда, согласно определению 7, матрица 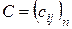 , где
, где
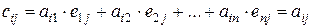 , так как
, так как 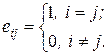
Пусть матрица 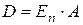 , тогда, согласно определению 7, матрица
, тогда, согласно определению 7, матрица 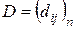 , где
, где
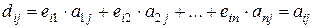 , так как
, так как 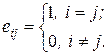
Из полученных результатов следует, что 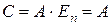 и
и 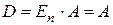 , следовательно,
, следовательно, 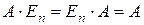 . Утверждение доказано.
. Утверждение доказано.
Следствие 1. Если матрица 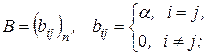 где
где 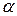 - некоторое число, т.е. B - cкалярная матрица порядка n, то для любой матрицы
- некоторое число, т.е. B - cкалярная матрица порядка n, то для любой матрицы 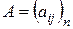
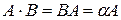 . (15)
. (15)
Доказательство. Нетрудно заметить, что  . Следовательно,
. Следовательно,
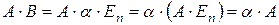 ;
; 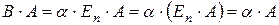 .
.
Что и требовалось доказать.
Определение 13. Операция перехода от матрицы 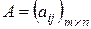 к матрице
к матрице 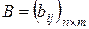 , где
, где 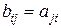 ,
, 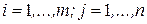 , т.е. когда столбцы матрицы А превращаются в соответствующие строки матрицы В, называется транспонированием матрицы А. Матрица В в этом случае называется транспонированной матрицей А.
, т.е. когда столбцы матрицы А превращаются в соответствующие строки матрицы В, называется транспонированием матрицы А. Матрица В в этом случае называется транспонированной матрицей А.
Обозначение: 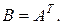
Пример 11. 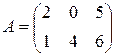 ,
, 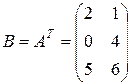 .
.
Замечание. Нетрудно заметить, что при транспонировании матриц элементы, стоящие на главной диагонали, не изменяю своего положения.
Теорема 3 (свойства операции транспонирования)
1) 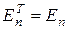 , где
, где 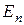 - единичная матрица порядка n.
- единичная матрица порядка n.
2) 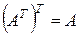 , для любых матриц
, для любых матриц 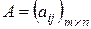 .
.
3) 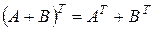 , где
, где 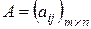 и
и 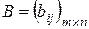 (16)
(16)
4) 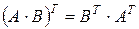 , где
, где 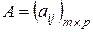 и
и  . (17)
. (17)
5) 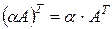 , для любых матриц А и любых постоянных
, для любых матриц А и любых постоянных 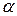 .
.
Доказательство. Справедливость свойств 1 и 2 следует из определения 13. Следовательно, доказать требуется лишь свойства 3 и 4.
3) Пусть 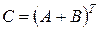 .
.
Так как 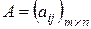 ,
, 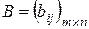 , то для матрицы
, то для матрицы 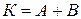 , где
, где 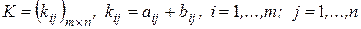 .
.
Следовательно, 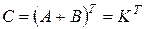 , и, согласно определению 13,
, и, согласно определению 13, 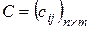 , где
, где
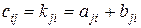 ,
, 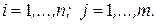 (18)
(18)
Пусть 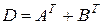 . Так как
. Так как 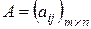 ,
, 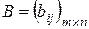 , то матрица
, то матрица 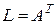 - матрица вида
- матрица вида 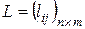 , где
, где 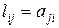 ,
, 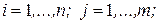 а матрица
а матрица 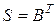 - матрица вида
- матрица вида 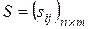 , где
, где 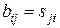 ,
, 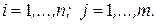
Следовательно, 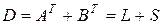 и
и 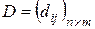 , где
, где
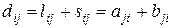 ,
, 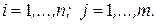 (19)
(19)
Из формул (18) и (19) следует, что 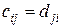 ,
, 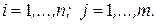 Это означает равенство матриц С и D, а значит, и справедливость формулы (16). Утверждение 3 доказано.
Это означает равенство матриц С и D, а значит, и справедливость формулы (16). Утверждение 3 доказано.
4) Применяем ту же методику: доказываем, что матрицы в левой и правой части равенства (17) состоят из одинаковых элементов.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
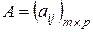 ,
,  , тогда
, тогда 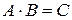 , где
, где 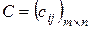 , элементы которой определяются по формуле (20):
, элементы которой определяются по формуле (20):
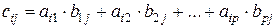 ,
, 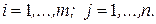 (20)
(20)
Пусть 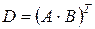 , тогда
, тогда 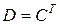 и, согласно определению 13,
и, согласно определению 13, 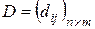 , где
, где 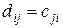 ,
, 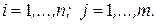 В этом случае, из (20) следует, что элементы матрицы определяются по формулам (21):
В этом случае, из (20) следует, что элементы матрицы определяются по формулам (21):
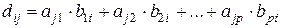 ,
, 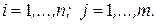 (21)
(21)
Так как 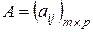 ,
,  , то матрица
, то матрица 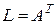 - матрица вида
- матрица вида 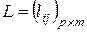 , где
, где 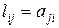 ,
, 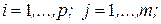 а матрица
а матрица 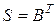 - матрица вида
- матрица вида 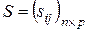 , где
, где 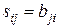 ,
, 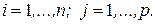
Следовательно, матрица 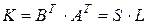 ,
, 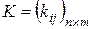 , элементы которой определяются по правилу:
, элементы которой определяются по правилу:
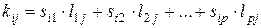 ,
, 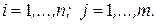 (22)
(22)
Используя представления элементов матриц L и S с помощью элементов матриц А и В, получаем:
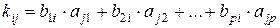 ,
, 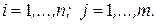 (23)
(23)
Из равенств (21) и (23) следует, что элементы матриц D и К, стоящие на одинаковых местах, совпадают, значит, 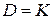 , что означает, что
, что означает, что 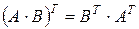 . Утверждение доказано.
. Утверждение доказано.
5) Данное свойство докажите самостоятельно.
Определение 14. Элементарными преобразованиями матриц называются следующие операции над матрицами:
1) перестановка двух строк матрицы местами;
2) умножение всех элементов некоторой строки матрицы на одно и то же число;
3) прибавление к элементам некоторой строки матрицы соответствующих элементов другой строки этой же матрицы, умноженных на число;
4) те же операции над столбцами.
Определение 15. Матрицы А и В, получающиеся одна из другой при помощи элементарных преобразований, называются эквивалентными.
Обозначение: 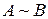 .
.
Смысл этой эквивалентности станет Вам понятен позднее, в частности, при исследовании систем линейных уравнений.
|
|
