Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!
Сгруппированного вариационного ряда (i—обычный способ, II—способ моментов)
|
|
| Возраст больного V | Число больных, Р | I способ | II способ | |||||||||
| Vp | D=V-M | dp | d2 | d2р | d=V-A | Dp | d2 | d2р | ||||
| -10, 3 | -10, 3 | 105, 09 | 103, 09 | -9, 0 | -9, 0 | 81, 0 | 81, 0 | |||||
| -8, 3 | -8, 3 | 68, 89 | 68, 89 | -7, 0 | -7, 0 | 49, 0 | 49, 0 | |||||
| -7, 3 | -29, 2 | 53, 29 | 213, 16 | -6, 0 | -24, 0 | 36, 0 | 144, 0 | |||||
| -6, 3 | -12, 3 | -72, 9 | 39, 69 | 79, 38 | -5, 0 | -10, 0 | -56, 0 | 25, 0 | 50, 0 | |||
| -3, 3 | -9, 9 | 10, 89 | 32, 67 | -2, 0 | -6, 0 | 4, 0 | 12, 0 | |||||
| -1, 3 | -2, 6 | 1, 69 | 3, 38 | 0, 0 | 0, 0 | 0, 0 | 0, 0 | |||||
| 0, 7 | 2, 8 | 0, 49 | 1, 96 | 2, 0 | 8, 0 | 4, 0 | 16, 0 | |||||
| 2, 7 | 8, 1 | 7, 29 | 24, 81 | 4, 0 | 12, 0 | 16, 0 | 48, 0 | |||||
| 4, 7 | 23, 5 | +72, 9 | 22, 09 | 110, 45 | 6, 0 | 30, 0 | +95, 0 | 36, 0 | 180, 0 | |||
| 6, 7 | 26, 8 | 44, 89 | 179, 56 | 8, 0 | 32, 0 | 64, 0 | 256, 0 | |||||
| 11, 7 | 11, 7 | 136, 89 | 136, 89 | 13, 0 | 13, 0 | 169, 0 | 169, 0 | |||||
| n=30 Σ Vp=1479 | Σ dp=0 | Σ d2 =954.3 | Σ dp=39 | Σ d2 p=1005 |
Средняя арифметическая имеет следующие свойства:
1) сумма отклонений от средней равна нулю (см. табл. 2, гр. 5);
2) при умножении (делении) всех вариант на один и тот же множитель (делитель) средняя арифметическая умножается (делится) на тот же множитель (делитель);
3) если прибавить (вычесть) ко всем вариантам одно и то же число, средняя арифметическая увеличивается (уменьшается) на то же число.
Эти свойства могут быть использованы для облегчения и упрощения расчета средней арифметической.
Первое свойство, например, служит обоснованием для расчета средней арифметической по способу моментов.
Как видно из табл. 2 (гр. 5), сумма всех отклонений вариант от средней равна нулю (отклонение d — это разность между каждой вариантой и средней величиной, т. е. d = V-M). Поскольку в сгруппированном вариационном ряду варианты имеют различную частоту, то каждая из них в итоге дает отклонения, зависящие от этой повторяемости. Следовательно, значение отклонения варианты необходимо умножить на частоту, а затем суммировать все эти произведения. Каждая варианта отклоняется от средней величины в большую или меньшую сторону со знаком «+» или «-». Эти значения следует учитывать при проведении вычислений. Сумма отрицательных отклонений равна -72, 9, сумма положительных отклонений составляет 72, 9, а итоговая сумма всех отклонений равна нулю (Σ dp = 0). Это свидетельствует о том, что средняя величина действительно есть общая количественная характеристика данного вариационного ряда, так как она взаимоисключает, взаимоуничтожает все отклонения. Это свойство положено в основу вычисления средней величины по способу моментов. Значение средней определяется по формуле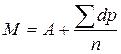 
, где А является условной средней величиной. Если А является истинной средней, т. е. А = М, то сумма ее отклонений будет равна нулю, если же она не является истинной средней, то сумма отклонений будет иметь значение, отличное от нуля, и явится основой для определения поправки. В табл. 2 (II способ) показаны этапы вычисления средней величины по способу моментов (А = 48). Из гр. 9 табл. 2 видно, что сумма отклонений Σ dp равна 39. С учетом поправки легко определить действительное значение средней величины, подставив соответствующие значения в формулу:
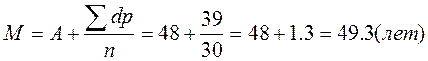
Таким образом, полученное значение средней арифметической величины по способу моментов идентично таковому, найденному обычным способом.
При выборе условной средней А следует ориентироваться на моду или медиану.
Способ моментов значительно упрощает расчеты и делает их более быстрыми.
Второе свойство средней арифметической полезно применять при анализе вариационного ряда, состоящего либо из очень больших, либо из очень малых величин. Имеются, например, варианты: 0, 0001; 0, 0002; 0, 0003. Используя это свойство, увеличим их в 10000 раз. Получим величины 1, 2, 3. Средняя арифметическая из них равна 2, а искомая средняя арифметическая в 10000 раз меньше, т. е. 0, 0002.
При обработке вариационного ряда, состоящего их положительных и отрицательных значений, иногда бывает полезно прибавить ко всем вариантам такое число, чтобы сделать их все положительными. Из полученного среднего результата эту величину следует вычесть. Например, имеются величины: +10, +5, -3, -1, +6, -1, -2. Определим среднюю арифметическую:
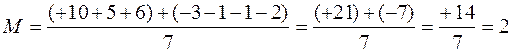
Чтобы избавиться от отрицательных величин, можно использовать третье свойство средней арифметической, т. е. прибавить к каждой варианте определенное число, например, в нашем случае 4. Тогда величины приобретут следующий вид: 14, 9, 1, 3, 10, 3, 2. Их сумма равна 42. При делении на 7 получим 6. При вычитании 4 из 6 получим среднюю арифметическую величину 2.
|
|