
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Використання графічної бібліотеки opengl 5 страница
|
|
Таблиця 12.9 – Можливі значення параметра pname команди glMaterial*()
| Значення параметра | Коментар |
| GL_AMBIENT | колір у форматі RGBA, що визначає розсіяний колір матеріалу (колір матеріалу у тіні), значення за замовчуванням: (0.2, 0.2, 0.2, 1.0) |
| GL_DIFFUSE | колір у форматі RGBA, що визначає колір дифузного віддзеркалення матеріалу, значення за замовчуванням: (0.8, 0.8, 0.8, 1.0) |
| GL_SPECULAR | колір у форматі RGBA, що визначає колір дзеркального відбиття матеріалу, значення за замовчуванням: (0.0, 0.0, 0.0, 1.0) |
| GL_SHININESS | ціле або дійсне значення у діапазоні [0, 128], що визначає ступінь дзеркального відбиття матеріалу, значення за замовчуванням: 0 |
| GL_EMISSION | колір у форматі RGBA, що визначає інтенсивність випромінюваного світла матеріалу, значення за замовчуванням: (0.0, 0.0, 0.0, 1.0) |
| GL_AMBIENT_AND_DIFFUSE | еквівалентно двом викликам команди glMaterial*() зі значеннями pname GL_AMBIENT та GL_DIFFUSE і однаковими значеннями params. |
Характер опису матеріалу об’єктів взаємодіє з параметрами освітлення. При вимкненому освітленні, колір вершини дорівнює поточному кольору, що встановлюється командами glColor*(). Увімкнення освітлення вершини забезпечує автоматичне обчислення кольорів вершин, виходячи з інформації про матеріал об’єкта, нормалі та джерела світла. Вимкнення освітлення прискорює візуалізацію, але кольори вершин автоматично не обчислюються і завдання розрахунків кольорів покладаються на розробника програми.
Якщо у сцені матеріали об’єктів розрізняються лише за одним параметром, спочатку встановлюється режим використання кольору матеріалу:
glEnable(GL_COLOR_MATERIAL);
Далі необхідно використовувати команду glColorMaterial():
void glColorMaterial (GLenum face, GLenum pname);
де параметри face і pname приймають ті самі значення, що і у функції glMaterial* ().
Після такої активації значення обраної властивості матеріалу встановлюються викликом команди glColor*(), що дозволяє уникнути викликів більш ресурсоємної команди glMaterial*() і тим самим підвищує ефективність програми.
Властивості матеріалу, зокрема можна визначити у такий спосіб:
float mat_dif[]={0.8, 0.8, 0.8};
float mat_amb[] = {0.2, 0.2, 0.2};
float mat_spec[] = {0.6, 0.6, 0.6};
float shininess = 0.7 * 128;
glMaterialfv (GL_FRONT_AND_BACK, GL_AMBIENT, mat_amb);
glMaterialfv (GL_FRONT_AND_BACK, GL_DIFFUSE, mat_dif);
glMaterialfv (GL_FRONT_AND_BACK, GL_SPECULAR, mat_spec);
glMaterialf (GL_FRONT, GL_SHININESS, shininess);
Нагадаємо, що у прикладі 12.9 червоний колір диску та сфери визначається властивостями матеріалу, а саме визначенням емісії:
GLfloat emission[]={1.0, 0.0, 0.0, 0.0}; // червоний колір емісії об’єктів
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
glMaterialfv(GL_FRONT, GL_EMISSION, emission); // увімкнення емісії
12.7.4 Використання ефекту туману
Не є секретом, що комп’ютерні доволі часто зображення є занадто чіткими і нереалістичними. Використання ефектів згладжування додає реалістичності з-за згладжування граней об’єктів. Ефект туману (fog) забезпечує плавне розмиття віддалених об’єктів. Взагалі, під загальною назвою “туман” у OpenGL імітують різні атмосферні ефекти: марево, імла, дим, забруднення. Ефект туману використовується тоді, коли необхідно імітувати обмежену видимість, зоктема у таких програмах, як авіасимулятори.
Якщо увімкнути режим туману, об’єкти по мірі їх віддалення від точки спостереження починають переходити у колір туману. Щільність туману можна керувати, для чого змінювати швидкість поступового змінення об’єктів по мірі змінення відстані. Туман (fog) реалізується шляхом зміни кольору об’єктів сцени у залежності від їх глибини, тобто відстані до точки спостереження. Зміна кольору відбувається або для вершин примітивів, або для кожного пікселя на етапі растеризації у залежності від реалізації OpenGL.
Туман впливає на перетворення освітлених та текстурованих об’єктів і застосовується до усіх типів графічних примітивів.
Туман має визначатися за допомогою команди glFog*() і вмикається за допомогою команди glEnable():
glEnable(GL_FOG);
За допомогою команди glFog*() обирається колір туману і визначаються рівняння щільності. Увімкнений режим туману змішує колір туману з кольором вхідного фрагмента, використовуючи коефіцієнт змішування туману у залежності від глибини об’єктів, тобто відстані до точки спостереження. Зміна кольору відбувається або для вершин примітивів, або для кожного пікселя на етапі растеризації у залежності від реалізації OpenGL.
Метод обчислення інтенсивності туману у вершині можна визначити за допомогою команд
void glFog[if] (enum pname, T param);
void glFog[if]v (enum pname, T params);
Для визначення параметрів туману необхідно вказати аргумент pname і вcтановити його значення у другий аргумент – параметр papam (або params). Параметр pname може приймати значення, вказані у таблиці 12.10.
Якщо у параметр param встановлюється значення GL_FOG_MODE, необхідно визначити спосіб обчислення інтенсивності туману у окремій точці сцени. У такому випадку param може приймати значення, наведені у таблиці 12.11.
Таблиця 12.10 – Опис основних параметрів туману
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
| Значення параметра | Коментар |
| GL_FOG_MODE | визначає формулу, за якою обчислюватиметься інтенсивність туману |
| GL_FOG_DENSITY | визначає щільність туману |
| GL_FOG_START | початок зони туману (використовується у лінійній характеристиці) |
| GL_FOG_END | кінець зони туману (використовується у лінійній характеристиці) |
Таблиця 12.11 – Визначення інтенсивності туману
| Значення параметра | Коментар |
| GL_EXP | Інтенсивність обчислюється за формулою 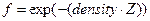 , де density – щільність, Z – відстань між точкою спостереження та центром фрагмента у системі координат спостерігача , де density – щільність, Z – відстань між точкою спостереження та центром фрагмента у системі координат спостерігача
|
| GL_EXP2 | Інтенсивність обчислюється за формулою  , де density – щільність Z – відстань між точкою спостереження та центром фрагмента у системі координат спостерігача , де density – щільність Z – відстань між точкою спостереження та центром фрагмента у системі координат спостерігача
|
| GL_LINEAR | Інтенсивність обчислюється за формулою 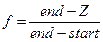 , де Z – відстань між точкою спостереження та центром фрагмента у системі координат спостерігача, end – визначається параметром GL_FOG_END, а start – параметром GL_FOG_START , де Z – відстань між точкою спостереження та центром фрагмента у системі координат спостерігача, end – визначається параметром GL_FOG_END, а start – параметром GL_FOG_START
|
Можна навести такий приклад використання туману: нехай на сцені зображено дерево і включено режим туману. Таким чином, із збільшенням відстані до дерева дія туману посилюватиметься. Для реалізації програми необхідно реалізувати такі кроки:
1) визначити розсіяне (ambient) освітлення сцени;
2) визначити параметри туману;
3) побудувати графічні об’єкти, що складатимуть дерево.
Відстань до дерева реалізуємо, як і у попередніх прикладах, за допомогою горизонтальної смуги прокручування.
Текст обробника OnOpenGLFirst() наводиться у прикладі 12.10, там також наведені необхідні коментарі до написаного коду. Результат роботи програми наведено на рисунку 12.10.
Приклад 12.10 – Код обробника із реалізацію туману
void CMain:: OnEighth()
{ glTranslatef (0.0, -5.0, 0.0); // зміщення сцени (для кращого відображення)
glTranslatef (0.0, 0.0, hspos-50.0); // зміна положення об’єктів
glEnable(GL_DEPTH_TEST); // увімкнено тест глибини
GLfloat light_ambient[]={1.0, 1.0, 1.0, 0.0}; // колір розсіяного світла
glLightfv (GL_LIGHT0, GL_AMBIENT, light_ambient); // встановлення розсіяного світла
glEnable (GL_LIGHTING); // увімкнення освітлення
glEnable(GL_LIGHT0); // увімкнення світла
GLfloat FogColor[4]={0.0, 0.0, 0.8, 0.0}; // колір туману
glFogi(GL_FOG_MODE, GL_LINEAR); // лінійний закон туману
glFogfv(GL_FOG_COLOR, FogColor); // встановлення кольору туману
glFogi(GL_FOG_DENSITY, 1.0); // встановлення щільності туману
glFogf(GL_FOG_START, 0.0); // початок зони туману
glFogf(GL_FOG_END, 10.0); // кінець зони туману
glEnable(GL_FOG); // увімкнення туману
GLUquadricObj *m_quadObj; // оголошення квадратичного об’єкта
m_quadObj=gluNewQuadric();
glRecti(0, 0, 1, 4); // «стовбур дерева»
glPushMatrix(); // збереження поточної СК
glTranslatef(-1.0, 4.0, 0.0); // переміщення у точку центра кола
gluDisk(m_quadObj, 0.0, 2.0, 80, 80); // відображення кола
glPopMatrix(); // повернення у базову CК
glPushMatrix();
glTranslatef(1.5, 4.0, 0.0); gluDisk(m_quadObj, 0.0, 1.5, 80, 80);
glPopMatrix();
glPushMatrix();
glTranslatef(1.5, 6.5, 0.0); gluDisk(m_quadObj, 0.0, 1.8, 80, 80);
glPopMatrix();
glPushMatrix();
glTranslatef(1.0, 8.0, 0.0); gluDisk(m_quadObj, 0.0, 1.0, 80, 80);
glPopMatrix();
glPushMatrix();
glTranslatef(-1.0, 7.0, 0.0); gluDisk(m_quadObj, 0.0, 1.5, 80, 80);
glPopMatrix();
}

а) б)
Рисунок 12.10 – Реалізація ефекту туману
(а – об’єкт віддалений у зону туману, б – наближений об’єкт)
12.7.5 Прозорість об’єктів та її використання
У реальному світі існує багато прозорих об’єктів – віконне скло, прозорий посуд тощо. З практичної точки зору важливим є вміння створювати такі прозорі об’єкти. Бібліотека OpenGL надає можливість механізму роботи з напівпрозорими об’єктами. Прозорість реалізується за допомогою змішування кольорів (blending). Алгоритм змішування комбінує кольори вхідних пікселів (тобто “кандидатів” на поміщення у буфер кадру) з кольорами відповідних пікселів, що вже зберігаються у буфері. Для змішування використовується четверта компонента кольору – альфа-компонента, тому цей режим інакше називають альфа-змішуванням. Програма може керувати інтенсивністю альфа-компоненти саме так, як інтенсивністю основних кольорів, тобто задавати значення інтенсивності для кожного пікселя або кожної вершини примітиву.
Режим змішування вмикається за допомогою команди glEnable():
glEnable(GL_BLEND);
Параметри змішування визначаються командою glBlendFunc():
void glBlendFunc (enum src, enum dst);
Параметр src визначає, яким чином отримується коефіцієнт k1 початкового кольору пікселя, a параметр dst задає спосіб отримання коефіцієнта k2 для кольору у буфері кадру. Сумарний колір розраховується за формулою:
res=сsrc· k1+cdst · k2,
де сsrc – колір початкового пікселя, cdst – колір пікселя у буфері кадру. Зазначимо, що усі перераховані параметри (res, k1, k1, сsrc, cdst) є чотирьохкомпонентними RGBA-векторами). Найбільш використовувані значення аргументів src и dst наведені у таблиці 12.12.
Таблиця 12.12 – Деякі значення констант режимів змішування
| Значення параметра | Коментар |
| GL_SRC_ALPHA | k=(As, As, As, As) |
| GL_SRC_ONE_MINUS_ALPHA | k=(1, 1, 1, 1)-(As, As, As, As) |
| GL_DST_COLOR | k=(Rd, Gd, Bd) |
| GL_ONE_MINUS_DST_COLOR | k=(1, 1, 1, 1)- (Rd, Gd, Bd, Аd) |
| GL_DST_ALPHA | k=(Ad, Ad, Ad, Ad) |
| GL_DST_ONE_MINUS_ALPHA | k=(1, 1, 1, 1)-(Ad, Ad, Ad, Ad) |
| GL_SRC_COLOR | k=(Rs, Gs, Bs) |
| GL_ONE_MINUS_SRC_COLOR | k=(1, 1, 1, 1)- (Rs, Gs, Bs, As) |
У таблиці 12.12 Rs, Gs, Bs, As означають відповідні кольори початкового пікселя (пікселя-джерела (source)), Rs, Gs, Bs, As – кольори цільового пікселя (destination).
Припустимо, що необхідно реалізувати виведення прозорих графічних об’єктів. Коефіцієнт прозорості задається альфа-компонентою кольору, для непрозорих об’єктів альфа-компонента дорівнює 1, для абсолютно прозорих, тобто невидимих, дорівнює 1. Для активізації прозорих властивостей необхідно увімкнути режим прозорості та визначити параметри змішування:
glEnable(GL_BLEND);
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
Напівпрозорі об’єкти можна задати визначивши альфа-параметр кольору, вищий за 0. У прикладі 12.11 наведено варіант обробника OnOpenGLFirst() із прозорими об’єктами – двома дисками (на основі квадратичних команд) та прямокутником. Результат використання такого обробника наведено на рисунку 12.11.
Приклад 12.11 – Приклад реалізації прозорих об’єктів
void CMain:: OnNineth()
{ glTranslatef(-1.0, -4.0, 0.0);
glRotatef(360.0*vspos/100, 1, 0, 0); // обертання навколо осі X
glTranslatef(0.0, 0.0, hspos-50.0);
glEnable(GL_DEPTH_TEST); // увімкнення тесту глибини
glEnable(GL_BLEND); // увімкнення режиму прозорості
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA); // режим змішування
GLUquadricObj *m_quadObj;
m_quadObj=gluNewQuadric();
glColor4f(1.0, 0.0, 0.0, 0.9); // альфа-параметр встановлено у 0.9
glRecti(0, 0, 4, 4); // прямокутник
glColor4f(0.0, 1.0, 0.0, 0.9);
glPushMatrix();
glTranslatef(-1.0, 4.0, 0.0);
gluDisk(m_quadObj, 0.0, 2.0, 80, 80); // диск
glPopMatrix();
glColor4f(0.0, 1.0, 1.0, 0.9);
glPushMatrix();
glTranslatef(1.5, 4.0, 0.0);
gluDisk(m_quadObj, 0.0, 1.5, 80, 80); // диск
glPopMatrix();
}
Якщо у сцені графічного виведення є декілька прозорих об’єктів, що перекриваються, коректний вивід можна гарантувати тільки за таких умов:
1) усі прозорі об’єкти виводяться після непрозорих;
2) виведення прозорих об’єктів має виконуватися упорядковано за зменшенням глибини, тобто виводитися, починаючи з об’єктів, що є найбільш віддаленими від спостерігача.
У OpenGL команди обробляються у порядку їх надходження, тому для реалізації перелічених вимог достатньо розставити виклики команд glVertex*() у відповідному порядку.

Рисунок 12.11 – Виведення сцени із прозорими об’єктами
У заключенні розділу слід сказати, що, звичайно, дуже складно на 50-ти сторінках розглянути технологію OpenGL і проілюструвати їх прикладами. Тому увагу звернуто на найбільш прості і, водночас, цікаві аспекти технології. Натомість, на наш погляд, вони дають уявлення про графічне програмування і забезпечують підґрунтя для більш ретельного вивчення.
12.8 Контрольні завдання
1. Навести основні характерні властивості графічної бібліотеки OpenGL.
2. Пояснити функціонування конвеєру візуалізації OpenGL.
3. Пояснити організацію графічного виведення у звичайних MFC-програмах.
4. Пояснити особливості організації графічного виведення у MFC-програмах із використанням команд OpenGL.
5. Пояснити організацію конструктора мінімальної OpenGL-програми, побудованої основі MFC-проекту.
6. Пояснити перетворення систем координат OpenGL під час виконання команд візуалізації.
7. Пояснити способи накладення текстур у OpenGL-програмах.
8. Реалізувати мінімальну OpenGL-програму на основі MFC-проекту.
9. Реалізувати обробник OpenGL-програми для побудови об’єктів типу куб, піраміда, конус на основі базових примітивів OpenGL.
10. Реалізувати обробник OpenGL-програми із побудовою об’єкта типу робот, забезпечите керування окремими суглобами роботами за допомогою регуляторів.
11. Реалізувати обробник OpenGL-програми із побудовою об’єкта типу ракета, забезпечити накладення текстур на поверхні ракети.
12. Реалізувати програму із прожектором – джерелом освітлення, забезпечити регулювання його робочих параметрів (розташування, напрям, кут освітлення).
13. Реалізувати програму із ефектом туману, забезпечити регулювання параметрів туману.
РОЗРОБКА СИСТЕМИ ПЛАНУВАННЯ РОБОТА
13.1 Системи планування та їх завдання
Як відомо, інтелектуальними (або інтегральними) роботами називають автоматичні пристрої третього покоління, що мають функціонувати у динамічному замкненому світі, мають тактильне та зорове сприйняття навколишньої дійсності, володіють можливостями мобільності та зміни зовнішнього простору. Окрім того, системи керування інтелектуальних роботів мають функціонувати на основі моделювання зовнішнього світу, вибору рішення завдання, виходячи з поставленої мети та динамічних змін у зовнішньому світі [12, 15].
Для забезпечення вирішення подібних проблем служать вирішувачі інтелектуальних завдань. Найбільш популярними розробками у цій галузі є GPS (General Problem Solver), який призначено для вирішення переважно математичних завдань та STRIPS (Stanford Research Institute Problem Solver), що з самого початку планувався як система планування завдань адаптивних (а потім інтелектуальних) роботів.
Системи планування інтелектуальних роботів у своїй основі ґрунтуються на розробках інтелектуальних вирішувачів. Побудова теорії інтелектуальних вирішувачів передбачає вирішення двох проблем: 1) опис вирішувача, його знань та діяльності [1, 6]; 2) побудова теорії інтелектуальних рішень [12].
Вирішення інтелектуальних завдань в наш час практично є прерогативою людини. Вочевидь, людина користується своєю внутрішньою мовою подання знань, що дозволяє їй спрощувати модель свого внутрішнього світу та здійснювати за їх допомогою ефективний пошук необхідних рішень у тісній взаємодії із достатньо повно описаною моделлю зовнішнього світу. Таким чином при побудові вирішувача необхідно описувати не тільки моделі вирішувача, але й модель функціонування людини у процесі прийняття рішень.
Опис системи планування – це в першу чергу опис закономірностей розумової діяльності такої системи при розв’язанні складних проблемних завдань. Ця діяльність має включати процеси усвідомлення системою планування ситуацій зовнішнього світу та виконуваних дій, також процеси пошуку рішень завдань. Таким чином, опис системи планування, її знань та діяльності, має містити [12]:
1) опис виконавчих органів вирішувача;
2) опис зовнішнього середовища;
3) опис знань системи планування, що відображають розуміння діяль-ності виконавчих органів і навколишнього середовища вирішувача;
4) опис процесів пошуку рішень запропонованих завдань.
Звідси виходить, що проблема опису інтелектуальних вирішувачів потребує створення більш потужного апарату опису у порівнянні з описуваними засобами класичної математики. Цей апарат має забезпечувати [13]:
1) подання знань мовою, близькою до природної (із урахуванням семантичних та прагматичних аспектів);
2) можливість опису розумової діяльності системи планування;
3) можливість органічного поєднання кількісних та якісних аспектів у стратегіях пошуку рішень;
4) системність, тобто можливість опису діяльності вирішувача одночасно на усіх рівнях фіксованої ієрархії;
5) цілеспрямованість, тобто прив’язку діяльності вирішувача до кінцевого результату – мети діяльності;
6) можливість пошуку припустимих рішень;
7) ефективних підхід до машинно-орієнтованих мов високого рівня.
13.2 Загальні аспекти побудови систем планування
Практична реалізація плануючих систем має передбачати наявність самої підсистеми планування та виконавчої підсистеми. Так система STRIPS за задумом має працювати у реальному світі у взаємодії із виконавчою системою PlanEx (plan execution – виконання планів).
Проблемне середовище системи планування містить модель світу, набір операторних схем та мету (або набір цілей) системи. У випадку постановки задачі для мобільного робота у замкненому просторі світ робота має відповідати схемі розташування об’єктів у цьому просторі, наприклад рисунку 13.1.
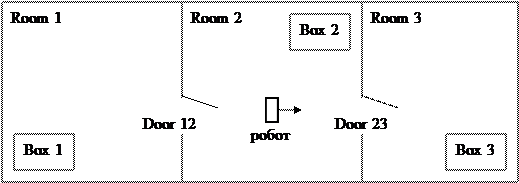 |
Рисунок 13.1 – Приклад схеми розташування об’єктів
для системи планування робота
Для вирішення практичних завдань необхідно автоматично формувати абстрактні простори різних рівнів з базового простору об’єктів та подій, у якому функціонує система.
У STRIPS-подібних системах [12, 13] абстракті простори визначаються рівнем деталізації умов застосування операторів. Такий підхід дозволяє:
1) залишати незмінною модель світу – немає необхідності викреслювати з неї несуттєві (для даного рівня абстракції) деталі та не враховувати їх;
2) залишати незмінними операторні схеми.
Модель світу подається у вигляді набору правильно побудованих формул (ППФ) логіки предикатів першого порядку, що відображають собою факти (наприклад, ATR(a) – робот знаходиться у пункті a) та закони, наприклад:
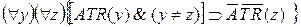 ,
,
тобто робот не може знаходитися одночасно у пунктах y та z.
Операторна схема визначається найменуванням, списком параметрів та описами у вигляді ППФ мови логіки предикатів першого порядку умов застосування дій та результату дії. Останній, у свою чергу містить список викреслювань та список додавання. Оператори породжують різні моделі світу шляхом генерування нових фактів. Мета системи також подається у вигляді ППФ тієї самої логіки, тобто вона є бажаною ППФ системи.
У системі STRIPS пошук починається зі спроби вивести цільову формулу G0 з вихідної моделі світу M0. Для цього програма доказу теорем здійснює пошук протиріччя у множині диз’юнктів  . Якщо таке протиріччя знайдене (виводиться пустий диз’юнкт), то вихідне завдання вирішується на цьому кроці тривіальним чином, тобто вихідна модель M0 задовольняє цілі G0. Якщо ж вказане протиріччя не погоджується, формується так званий незавершений вивід D0. Цей вивід подається набором диз’юнктів, відповідних запереченню формули мети (у даному випадку
. Якщо таке протиріччя знайдене (виводиться пустий диз’юнкт), то вихідне завдання вирішується на цьому кроці тривіальним чином, тобто вихідна модель M0 задовольняє цілі G0. Якщо ж вказане протиріччя не погоджується, формується так званий незавершений вивід D0. Цей вивід подається набором диз’юнктів, відповідних запереченню формули мети (у даному випадку  ), плюс усі їх похідні, якщо такі є, мінус ті диз’юнкти, що виключаються завдяки застосуванню обмежуючих стратегій (наприклад стратегій заміщення та оцінки предикатів).
), плюс усі їх похідні, якщо такі є, мінус ті диз’юнкти, що виключаються завдяки застосуванню обмежуючих стратегій (наприклад стратегій заміщення та оцінки предикатів).
Незавершений вивід D0 приймається різницею між M0 та G0, що позв’язується з даним вузлом (M0, G0). Далі відбувається пошук операторів, які підходять для зменшення отриманої різниці. Це такі оператори, дія яких на модель середовища дозволяє продовжувати доказ. При пошуку оператора, який підходить, значення його параметрів піддаються частковому або повному перебору.
Пошук оператора складається з двох кроків. На першому кроці складається упорядкований список операторів-кандидатів. Вибір операторів-кандидатів оснований на простому порівнянні предикатів з різниці D0 з предикатами зі списку доповнення оператора. Другий крок полягає у застосуванні програми доказу теорем для визначення того, чи є у вказаному списку доповнень диз’юнкти, що могли б продовжити вивід після застосування цього оператора. Якщо цей крок видався успішним, оператор-кандидат із відповідними значеннями параметрів розглядається як підходящий для зменшення різниці D0.
Коли таким чином оператор-кандидат знайдений, умови його застосування приймаються як нові підцілі системи. Нехай перед роботом поставлене завдання – перейти у точку b. Тоді G0 =ATR(b) й до тих пір, поки робот не опиниться у точці b, спроби знайти необхідний доказ виявляться марними. Вочевидь, що окремий випадок goto(m, b) оператора goto(m, n) – перейти з пункту m у пункт n – підходить для зменшення різниці  , оскільки результат - ATR(b) дозволяє продовжити вивід G0 (у даному випадку - і закінчити його). Роль нової підцілі G1 гратиме відповідна схема ППФ – умова застосування, скажімо ATR(m).
, оскільки результат - ATR(b) дозволяє продовжити вивід G0 (у даному випадку - і закінчити його). Роль нової підцілі G1 гратиме відповідна схема ППФ – умова застосування, скажімо ATR(m).
Система STRIPS поступає з підціллю G1 так само, як і з метою. Вона знову використовує доказ теорем для виведення G1 з M0. Тут важливі два випадки. Якщо система не знаходить доказ, вона аналогічним чином формує різницю D1 між M0 та G1 та встановлює підцілі, відповідні формулам умов застосування відповідних операторів-кандидатів. Якщо теорема виводить G1 з M0, то відпо-відний окремий випадок оператора використовується для перетворення моделі M0 у нову модель M1. У вищезгаданому простому прикладі підціллю є G1 =ATR(m). Якщо 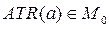 , окремий випадок G1, а саме ATR(a), може бути виведений з M0. У цьому випадку оператор goto(a, b) застосовується до моделі M0 й формує модель M1, що включає ATR(b). Потім STRIPS продовжує спроби вивести G0 з M1. У нашому прикладі G0 тривіально випливає з M1. Однак, якщо вивід G0 не вдається, встановлюються відповідні підцілі й процедура починається знову [12].
, окремий випадок G1, а саме ATR(a), може бути виведений з M0. У цьому випадку оператор goto(a, b) застосовується до моделі M0 й формує модель M1, що включає ATR(b). Потім STRIPS продовжує спроби вивести G0 з M1. У нашому прикладі G0 тривіально випливає з M1. Однак, якщо вивід G0 не вдається, встановлюються відповідні підцілі й процедура починається знову [12].
Ієрархію цілей, підцілей та моделей, породжувану у процесі пошуку, можна подати у вигляді дерева пошуку. Кожна вершина такого дерева має вигляд (модель середовища, (список підцілей)) і відповідає завданню досягнення (відповідно порядку) під цілей цільового списку з вказаної моделі середовища. Приклад дерева пошуку наведено на рисунку 13.2.
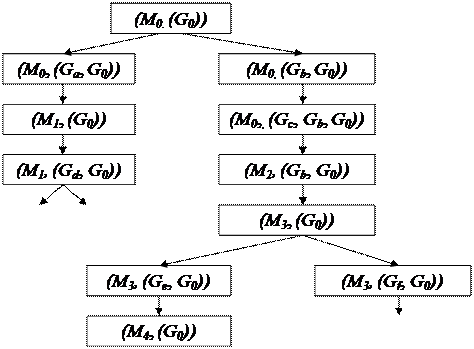 |
Рисунок 13.2 – Дерево пошуку у системі STRIPS
У прикладі дерева пошуку верхня вершина (M0, (G0)) є вихідним завданням: досягнути G0 з M0. У даному випадку встановлюються дві альтернативні підцілі Ga та Gb. Вони додаються у дві наступні дочірні вершини на початку цільового списку. Обравши ліву гілку припустимо, що у вершині (M0, (Ga, G0)) мета Ga задовольняється у M0 й тоді відповідний оператор, скажімо fa застосовується у M0 для отримання моделі M1 і завдання полягатиме у тому, щоб мета G0 задовольнялася у моделі M1. Це завдання подається вершиною (M1, (G0)).
Крокуючи іншим шляхом, отримаємо вершину (M4, (G0)). Припустимо, що формула-мета G0 задовольняється у M4, тобто вершина (M4, (G0)) є кінцевою. Тоді послідовність операторів fс, fb, fe є розв’язком завдання.
13.3 Реалізація систем планування
Практична реалізація описаних вище схем, включає її компоненти: модель світу, операторні схем та ціль системи. Зокрема мовою Prolog модель світу, відповідна рисунку 13.1 може бути описана набором тверджень:
is_a(room1, room, always)
|
|
