
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Використання графічної бібліотеки opengl 2 страница
|
|
pfd.dwFlags = PFD_DOUBLEBUFFER | PFD_SUPPORT_OPENGL | PFD_DRAW_TO_WINDOW;
pfd.iPixelType = PFD_TYPE_RGBA;
pfd.cColorBits = 24;
pfd.cDepthBits = 32;
pfd.iLayerType = PFD_MAIN_PLANE;
CClientDC dc(this);
int nPixelFormat = ChoosePixelFormat(dc.m_hDC, & pfd);
BOOL bResult = SetPixelFormat(dc.m_hDC, nPixelFormat, & pfd);
m_hrc = wglCreateContext(dc.m_hDC);
wglMakeCurrent(dc.m_hDC, m_hrc);
CreateRGBPalette(dc.m_hDC);
m_pPal = NULL;
}
BOOL CApp:: InitInstance()
{m_pMainWnd= new CMain;
m_pMainWnd-> ShowWindow(m_nCmdShow);
m_pMainWnd-> UpdateWindow();
return TRUE; }
CApp App;
BEGIN_MESSAGE_MAP(CMain, CFrameWnd)
ON_COMMAND(ID_OPENGL_FIRSTITEM, OnOpenGLFirst)
ON_WM_PAINT()
ON_WM_VSCROLL()
ON_WM_HSCROLL()
ON_WM_SIZE()
END_MESSAGE_MAP()
BOOL CMain:: CreateRGBPalette(HDC hDC)
{ PIXELFORMATDESCRIPTOR pfd;
int n = GetPixelFormat(hDC);
DescribePixelFormat(hDC, n, sizeof(PIXELFORMATDESCRIPTOR), & pfd);
if (! (pfd.dwFlags & PFD_NEED_PALETTE)) return FALSE;
LOGPALETTE* pPal = (LOGPALETTE*) malloc(sizeof(LOGPALETTE)
+ 256 * sizeof(PALETTEENTRY));
if (! pPal){TRACE(" Out of memory for logpal"); return FALSE; }
pPal-> palNumEntries = 256;
BOOL bResult = m_pPal-> CreatePalette(pPal);
free (pPal);
return bResult;
}
void CMain:: OnPaint()
{ CPaintDC pDC(this);
CPalette* ppalOld = NULL;
if (m_pPal) {ppalOld = pDC.SelectPalette(m_pPal, 0); pDC.RealizePalette(); }
BOOL bResult = wglMakeCurrent(pDC.m_hDC, m_hrc);
GLInit();
OnOpenGLFirst();
SwapBuffers(pDC.m_hDC);
if (ppalOld) pDC.SelectPalette(ppalOld, 0);
wglMakeCurrent(NULL, NULL);
}
void CMain:: OnSize(UINT nType, int cx, int cy)
{ CClientDC dc(this);
BOOL bResult = wglMakeCurrent(dc.m_hDC, m_hrc);
GLdouble gldAspect = (GLdouble) cx/ (GLdouble) cy;
glMatrixMode(GL_PROJECTION); // OutputGlError(" MatrixMode");
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
glLoadIdentity();
gluPerspective(30.0, gldAspect, 1.0, 10.0);
glViewport(0, 0, cx, cy);
wglMakeCurrent(NULL, NULL);
}
void CMain:: OnVScroll(UINT SBCode, INT Pos, CScrollBar *SB)
{switch(SBCode)
{case SB_LINEDOWN: vspos++; break;
case SB_LINEUP: vspos--; break;
case SB_PAGEDOWN: vspos+=5; break;
case SB_PAGEUP: vspos-=5; break;
case SB_THUMBTRACK: vspos=Pos; break;
case SB_THUMBPOSITION: vspos=Pos; break; }
Invalidate(FALSE);
SetScrollPos(SB_VERT, vspos);
}
void CMain:: OnHScroll(UINT SBCode, INT Pos, CScrollBar *SB)
{switch(SBCode)
{case SB_LINERIGHT: hspos++; break;
case SB_LINELEFT: hspos--; break;
case SB_PAGERIGHT: hspos+=5; break;
case SB_PAGELEFT: hspos-=5; break;
case SB_THUMBTRACK: hspos=Pos; break;
case SB_THUMBPOSITION: hspos=Pos; break; }
Invalidate(FALSE);
SetScrollPos(SB_HORZ, hspos);
}
void CMain:: GLInit()
{ static GLdouble marengo[3] = {1.0, 0.0, 0.0 };
glClearColor(1.0, 1.0, 1.0, 0.0);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
glTranslated(0.15, 0.15, -4.5);
glColor3dv(marengo);
glScalef(1.0, 1.0, 1.0);
}
void CMain:: OnOpenGLFirst()
{ glRotatef(360.0*hspos/100, 0, 1, 0); // 3D-scrolling around y
glRotatef(360.0*vspos/100, 1, 0, 0); // 3D-scrolling around x
auxWireTeapot(1.0); }
Розроблена у цьому підрозділі програма може стати основою для подальших розробок. Надалі програми конструюватимуться, в основному, додаванням до цієї програми-основи.
12.4 Основні команди відображення графічних примітивів
12.4.1 Синтаксис команд та основні типи OpenGL
Функції та процедури OpenGL, зазвичай, називають командами [5]. Команди OpenGL легко впізнати, навіть, якщо вони використовуються іншою системою або навіть мовою програмування. Вони мають спільні особливості.
Усі команди OpenGL мають префікс gl, а кожна назва функції починається з великої літери, наприклад glColor(), glPushMatrix(). Узагальнено команду OpenGL можна записати у такий спосіб:
rtype CommandName [1 2 3 4] [b s i f d us ui] [v] (atype arg)
у такому записі окремі частини означають таке:
CommandName – ім’я OpenGL-команди, наприклад glVertex;
[1 2 3 4] – кількість аргументів команди;
[b s i f d us ui] – тип аргументів команди (значення наведені у Таблиці 12.3);
[v] – літера, що вказує наявність покажчика на масив у аргументі команди.
Параметр rtype визначає тип значення, що повертається і для кожної команди вказується у явний вигляд. Параметр atype та аргумент arg визначаються типом та кількістю аргументів, відповідно.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Таблиця 12.3 – Позначення типів OpenGL та відповідні типи С++
| символ | тип OpenGL | тип С (С++) |
| b | GLbyte | char |
| s | GLshort | short |
| i | GLint | int |
| f | GLfloat | float |
| d | GLdouble | double |
| ub | GLbyte | byte |
| us | GLshort | short |
| ui | GLuint | Uint |
Таким чином команди OpenGL є складеними записами, зовнішній вигляд яких дозволяє дізнатися про кількість та тип застосовуваних параметрів. Кожна OpenGL-команда може визначати декілька перевантажених варіантів, наприклад, команда визначення вершин glVertex() має такі варіанти:
glVertex2d, glVertex2f, glVertex2i, glVertex2s, glVertex3d, glVertex3f, glVertex3i, glVertex3s, glVertex4d, glVertex4f, glVertex4i, glVertex4s, glVertex2dv, glVertex2fv, glVertex2iv, glVertex2sv, glVertex3dv, glVertex3fv, glVertex3iv, glVertex3sv,
glVertex4dv, glVertex4fv, glVertex4iv, glVertex4sv
Нижче наведено детальні прототипи двох прикладів зі списку:
void glVertex2f(float arg1, float arg2);
void glVertex3s(short arg1, short arg2, short arg3);
Перший приклад містить два аргументи плаваючого (float) типу, другий – три короткого цілого (int) типу.
Назви констант OpenGL записуються виключно великими літерами, наприклад GL_COLOR_BUFFER_BIT. Константи OpenGL-команд будуть надалі описуватися у необхідних випадках.
12.4.2 Команди відображення графічних примітивів OpenGL
Як вже зазначувалося вище, вершини графічних об’єктів OpenGL визначаються за допомогою команди glVertex*(). У формальний спосіб її прототипи описуються у такий спосіб:
void glVertex [2 3 4] [s i f d](type coord);
void glVertex [2 3 4] [s i f d] v (type coord);
Виклик будь-якої команди типу glVertex*() визначається чотирма координатами: x, y, z та w. При цьому якщо, наприклад використовується команда glVertex2() задаються лише координати x та y, а значення z та w є фіксованими: z =0, w=1. Виклик glVertex3() потребуватиме завдання x, y, z і фіксує w=1. Виклик glVertex4() задаватиме усі чотири координати. Додатково зазначимо, що використання параметра w забезпечує врахування впливу перспективи.
Примітивом OpenGL вважається простий графічний об’єкт (точка, лінія, багатокутник, растрове зображення), яким можна маніпулювати як єдиною дискретною сутністю [5]. Для примітивів може встановлюватися ряд параметрів, серед яких – колір.
Поточний колір графічного об’єкта разом з умовами освітлення визначає його поточний сумарний колір. Колір задається двома командами:
void glColor [3 4] [b s i f d][v] (GLtype components); // встановлення RGBA-кольору
void glIndex [3 4] [s i f d] v (GLtype index); // індексний режим кольору
Зазвичай використається RGBA-режим встановлення кольору. Цей режим використовує червоне, зелене та синє значення кольорів (відповідно R, G, B) для визначення кольору пікселя на екрані. Значення інтенсивності кольорів встановлюються у діапазоні [0.0, 1.0]. Наприклад:
glColor3f (0.0, 0.0, 0.0); // чорний колір
glColor3f (1.0, 0.0, 0.0); // червоний
glColor3f (0.0, 1.0, 0.0); // зелений
glColor3f (0.0, 0.0, 1.0); // синій
glColor3f (1.0, 1.0, 0.0); // жовтий
glColor3f (1.0, 1.0, 1.0); // білий
Значення альфа-параметра (A) не приймає участі формуванні результуючого кольору, а визначає ступінь прозорості: 0.0 – повна прозорість, 1.0 – повна непрозорість.
Після того, як певний колір встановлено як поточний, цей колір поширюється на всі пізніше створювані примітиви – до встановлення нового.
За допомогою наборів вершин задаються примітиви або групи однотипних примітивів: точки, лінії, з’єднані лінії, замкнені лінії, трикутники різного типу – із пов’язаними вершинами або ребрами, позв’язані та непозв’язані чотири- та інші багатокутники. Для формування набору послідовність точок розміщується всередині комбінації команд glBegin() / glEnd():
void glBegin (GLenum mode); // початок послідовності
void glEnd (); // кінець послідовності
Параметр mode встановлює графічний об’єкт, що є результатом послідовності вказаних вершин. Значення mode наведено у таблиці 12.4.
Таблиця 12.4 – Значення параметра mode команди glBegin()
| Значення mode | Результат застосування |
| GL_POINTS | кожна вершина розглядається як окрема незалежна точка |
| GL_LINES | пара вершин розглядається як незалежний відрізок (перша пара – перший відрізок, друга – другий і т.д.). Остання непарна вершина ігнорується. |
| GL_LINE_STRIP | послідовність з одного або декількох зв’язаних відрізків. Перша вершина – початок першого відрізка; друга – кінець, одночасно – початок другого відрізка і т.д. (N-1) відрізків. |
| GL_LINE_LOOP | аналогічний режиму GL_LINE_STRIP. Додатково: остання вершина замикається відрізком на першу. N відрізків. |
| GL_TRIANGLES | кожна трійка вершин формує незалежний трикутник. Якщо кількість вершин не є кратною 3, решта вершин (1 або 2) ігноруються. |
| GL_TRIANGLE_STRIP | група зв’язаних трикутників, що мають спільні грані: (1, 2, 3) – перший трикутник; (2, 3, 4) – другий трикутник і т.д. (N-2) трикутників. |
| GL_TRIANGLE_FAN | група зв’язаних трикутників, що формують веєр із спільною вершиною 1: (1, 2, 3) – перший трикутник; (1, 3, 4)– другий трикутник і т.д. (N-2) трикутників. |
| GL_QUADS | кожна четвірка вершин формує незалежний чотирикутник: (1, 2, 3, 4) – перший, (5, 6, 7, 8) – другий і т.д. Якщо кількість вершин не є кратною 4, решта вершин (1, 2, 3) ігноруються. N/4 чотирикутників. |
| GL_QUAD_STRIP | група зв’язаних чотирикутників, що мають спільні грані: (1, 2, 4, 3) – перший, (3, 4, 6, 5) – другий і т.д. Якщо N – непарне число, остання вершина ігнорується. |
| GL_POLYGON | багатокутник, що будується на послідовності точок (> 3). Багатокутник має не перетинати сам себе і має бути опуклим. |
Всередині комбінації команд glBegin() / glEnd() окрім самих вершин встановлюються додаткові параметри: колір, вектор нормалі, координати текстури, властивості матеріалу, також виконувати виклик списків. Використання інших команд не допускається.
За замовчуванням точка відображується на екрані як окремий піксель, а відрізок лінії також має ширину 1 піксель. Ситуацію можна змінити функціями glPointSize() та glLineWidth():
void glPointSize (GLfloat size); // size – ширина точки у пікселях
void glLineWidth (GLfloat width); // width – ширина лінії у пікселях
У прикладі 12.2 розглянуто варіант функції OnOpenGLFirst(), де послі-довності точок задаються всередині комбінацій glBegin() / glEnd().
Приклад 12.2 – Використання комбінацій функцій glBegin() / glEnd()
void CMain:: OnOpenGLFirst()
{ double pi=3.1415926535898; // число π
glRotatef(360.0*hspos/100, 0, 1, 0); // 3D-обертання навколо осі y
glRotatef(360.0*vspos/100, 1, 0, 0); // 3D- обертання навколо осі x
glColor3f(1.0, 0.0, 0.0); // червоний колір
glBegin(GL_POLYGON); // побудова багатокутника
glVertex3f(-5.0f, 5.0f, 5.0f);
glVertex3f(-5.0f, -5.0f, 5.0f);
glVertex3f(5.0f, -5.0f, 5.0f);
glVertex3f(5.0f, 5.0f, 5.0f);
glEnd();
glColor3f(0.0, 1.0, 0.0); // зелений колір
glBegin(GL_TRIANGLES); // побудова трикутників
glVertex2i(-2, 2);
glVertex2i(1, 6);
glVertex2i(5, 4);
glVertex2i(-2, -3);
glVertex2i(2, -3);
glVertex2i(4, 2);
glEnd();
glColor3f(1.0, 1.0, 0.0); // жовтий колір
glLineWidth(5.0); // ширина лінії – 5.0
glBegin(GL_LINE_LOOP); // послідовність відрізків, що складатиме коло
for(int i=0; i< 100; i++)
{double angle=2*pi*i/100;
glVertex2f(5.0*cos(angle), 5.0*sin(angle));
}
glEnd();
}
Результат роботи функції зображено на рисунку 12.3.
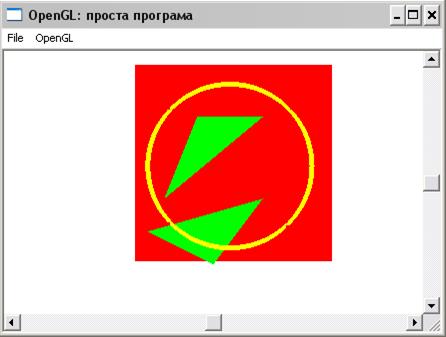
Рисунок 12.3 – Приклад побудови примітивів
Побудову прямокутників можна здійснити і більш простим способом, використавши спеціальну команду glRect*():
void glRect[d f i s] (type X1, type Y1, type X2, type Y2);
Команда glRect*() для роботи потребує вказання двох діагональних вершин прямокутника – (X1, Y1) та (X2, Y2). По суті записи glRecti(x1, y1, x2, y2) та
glBegin(GL_POLYGON);
glVertex2i(x1, y1);
glVertex2i(x2, y1);
glVertex2i(x2, y2);
glVertex2i(x1, y2);
glEnd();
є еквівалентними.
Наприклад, якщо необхідно побудувати синій прямокутник із діагональними вершинами (3.0, 3.0) та (6.0, 6.0), можна написати такий код:
glColor3f(0.0, 0.0, 1.0);
glRectf(3.0, 3.0, 6.0, 6.0);
Для отримання пунктирних або штрих-пунктирних ліній використовується команда glLineStipple(), що задає шаблон штрихування:
void glLineStipple(GLint factor, GLushort pattern);
де factor – масштабний коефіцієнт, що дозволяє розтягувати наявний шаблон (значеннями від 1 до 256), а pattern – 16-розрядна послідовність нулів та одиниць, яка становить шаблон побудови штрихування лінії. Зокрема, лінія з точок задається значенням 0x0101, пунктирна лінія – 0x00FF, штрих-пунктирна лі- нія – 0x1C47. Для використання штрихування необхідно за допомогою функції glEnable() включити відповідний режим роботи OpenGL-програми.
12.4.3 OpenGL як кінцевий автомат
Графічна система OpenGL є кінцевим автоматом. Цей автомат може переводитися у різні стани та залишатися у певному стані, доки цей стан не буде змінено новою командою.
За допомогою спеціальних змінних стану забезпечується керування кольором об’єктів, поточною візуалізацією, перетвореннями проекцій, шаблонами штрихування ліній, режимами введення багатокутників, пакування пікселів, контролювати властивості матеріалів, встановлювати розташування та визначати режими роботи джерел освітлення тощо.
За замовчуванням більшість режимів є неактивними. Активізація режимів роботи може призводити до уповільнення швидкості візуалізації, хоча і забезпечуватиме підвищення якості зображень.
Для увімкнення та вимкнення режимів використовуються прості команди:
void glEnable(GLenum cap);
void glDisable(GLenum cap);
Константа cap і є тим параметром стану OpenGL, що необхідно увікнути або вимкнути. OpenGL містить більше 40 таких параметрів контролю стану. Серед них такі:
GL_BLEND – керування змішуванням значень кольорів RGBA;
GL_DEPTH_TEST – керування тестом глибини;
GL_FOG – керування туманом;
GL_LINE_STIPPLE – штрихування ліній;
GL_TEXTURE_2D – робота з двовимірними текстурами;
GL_LIGHTING – керування освітленням.
Наприклад, командою glEnable(GL_LINE_STIPPLE) можна увімкнути штрихування ліній, а командою glDisable(GL_LIGHTING) вимкнути освітлення робочої сцени візуалізації.
За допомогою команди gllsEnabled() здійснюється перевірка стану:
GLboolean glIsEnabled(GLenum cap); // повертаються значення GL_TRUE та GL_FALSE
Параметром cap вказується константа, стан якої контролюється.
12.4.4 Формування списків зображень
Як видно з попередніх сторінок, програмний код побудови графічних об’єктів, що складаються з великої кількості вершин, є досить об’ємним, особливо, якщо однакові об’єкти доводиться будувати декілька разів. З метою оптимізації виконання таких однакових ділянок коду у OpenGL пропонується використання списків зображень. Список зображень є групою команд OpenGL, що збережена для подальшого виконання.
Використання списків зображень дозволяє поліпшити продуктивність програми, забезпечити кешування команд та їх збереження для подальшого виконання, оптимізувати матричні операції. Крім того, застосування списків зображень дозволяє забезпечити компіляцію растрових зображень, що використовуються у програмі, прискорити відображення освітлених сцен із джерелами освітлення та визначеними властивостями матеріалів і моделями розповсюдження світла, максимізувати ефективність обробки текстур.
Для роботи зі списком слід визначити ім’я списку, обмежити за допомогою спеціальних команд початок та кінець списку.
Кожен список ідентифікується цілочисельним індексом. Неспівпадаючі індекси генеруються командою glGenLists():
GLuint glGenLists(GLsizei range);
де range – кількість суміжних номерів індексів списків зображень.
Команди glNewList() та glEndList() визначають, відповідно, початок та кінець списку зображень:
void glNewList(GLuint list, GLenum mode);
void glEndList(void);
де list – ідентифікатор списку, mode – режим формування списку. Режим формування має два значення: GL_COMPILE (список компілюється без виконання) та GL_COMPILE_AND_EXECUTE (список компілюється і одразу виконується). Між викликами команд glNewList() та glEndList() розміщується, власне, перелік команд, що мають включатися у список. Можна, наприклад, побудувати список побудови чотирьох сторін куба:
GLuint Cube; // оголошення змінної - ідентифікатора списку
Cube=glGenLists(1); // генерація ідентифікатора списку
glNewList(Cube, GL_COMPILE); // початок списку
glBegin(GL_POLYGON);
glVertex3f(5.0f, 5.0f, 5.0f); glVertex3f(5.0f, -5.0f, 5.0f);
glVertex3f(5.0f, -5.0f, -5.0f); glVertex3f(5.0f, 5.0f, -5.0f);
glEnd();
glBegin(GL_POLYGON);
glVertex3f(-5.0f, 5.0f, -5.0f); glVertex3f(-5.0f, -5.0f, -5.0f);
glVertex3f(-5.0f, -5.0f, 5.0f); glVertex3f(-5.0f, 5.0f, 5.0f);
glEnd();
glBegin(GL_POLYGON);
glVertex3f(-5.0f, -5.0f, 5.0f); glVertex3f(-5.0f, -5.0f, -5.0f);
glVertex3f(5.0f, -5.0f, -5.0f); glVertex3f(5.0f, -5.0f, 5.0f);
glEnd();
glBegin(GL_POLYGON);
glVertex3f(-5.0f, 5.0f, -5.0f); glVertex3f(-5.0f, 5.0f, 5.0f);
glVertex3f(5.0f, 5.0f, 5.0f); glVertex3f(5.0f, 5.0f, -5.0f);
glEnd();
glEndList(); // кінець списку
glCallList(Cube); // виклик списку
Як видно з прикладу, виклик раніше підготовленого списку здійснюється за допомогою функції glCallList():
void glCallList(GLuint list); // list – ідентифікатор списку
Списки графічних зображень можуть складатися у списки більш високого рівня. Таким чином організація списків носитиме ієрархічний характер.
12.4.5 Функції побудови складених об’єктів
Реалізація OpenGL у Microsoft Windows оголошує (у заголовковому файлі glaux.h) наявність ряду функцій, що забезпечують побудову складених графічних об’єктів. Для усіх цих об’єктів існують версії функцій побудови каркасних та твердотільних тривимірних моделей. Каркасні функції тривимірних об’єктів наведено нижче, а твердотільні версії відрізняються лише наявністю складу Solid замість Wire. Інші операційні системи мають дещо інший склад функцій.
void auxWireSphere(GLdouble); // сфера
void auxWireCube(GLdouble); // куб
void auxWireBox(GLdouble, GLdouble, GLdouble); // призма
void auxWireTorus(GLdouble, GLdouble); // тор
void auxWireCylinder(GLdouble, GLdouble); // циліндр
void auxWireIcosahedron(GLdouble); // ікосаедр
void auxWireOctahedron(GLdouble); // октаедр
void auxWireTetrahedron(GLdouble); // тетраедр
void auxWireDodecahedron(GLdouble); // додекаедр
void auxWireCone(GLdouble, GLdouble); // конус
void auxWireTeapot(GLdouble); // чайник
12.5 Команди візуалізації OpenGL
12.5.1 Загальні відомості
Основним призначенням комп’ютерної графіки є створення двовимірного зображення тривимірних об’єктів. Це зображення має біти двовимірним з тієї причини, що будь-якому випадку екран комп’ютера є двовимірним.
Перетворення тривимірних координат об’єктів у піксельні точки на екрані включає операції моделювання, візуалізації або вибору кадру (viewing) та операції отримання проекцій. До таких операцій належать обертання (rotation), паралельне перенесення (translation), масштабування (scaling), дзеркальне відображення (reflecting), отримання ортогональних та перспективних проекцій [4]. Зазвичай використовується комбінація декількох перетворень для графічного виведення сцени.
Особливістю виконання команд візуалізації є і те, що оскільки виведення графічної інформації відбувається у прямокутне вікно, об’єкти (або частини об’єктів), що знаходяться за межами цього вікна, мають відсікатися. У тривімірній графіці відсікання виконується за допомогою відкидання об’єктів, що знаходяться по один бік площини відсічення.
Також має встановлюватися відповідність між перетвореними координатами та пікселями екрана. Вказана операція має назву перетворення порту перегляду (viewport).
Для отримання необхідної сцени під час візуалізації виконуються операції перетворення, що є аналогами отримання знімку за допомогою фотокамери. При цьому можна встановити перелік кроків отримання знімку [4]:
1) встановити штатив та направити камеру на сцену для вибору кадру або перетворення вигляду (view transformation);
2) встановити бажану композицію сцени, що фотографується, для перетворення моделі (modeling transformation);
3) оберіть об’єктив камери та визначте масштаб для перетворення проекції (project transformation);
4) визначте наскільки завеликою має бути кінцевий знімок для перетворення порту перегляду (viewport transformation).
Вказані етапи не обов’язково відповідають порядку, у якому виконуються відповідні математичні операції над вершинами об’єкта. На рисунку 12.4 наведено порядок здійснення таких операцій.

 |
Рисунок 12.3 – Етапи перетворення вершин
Для встановлення перетворення виду, моделювання та перетворення проекцій створюється матриця M розміру 4 x 4, що потім перемножується на координати кожної вершини ν на сцені під час виконання перетворення ν ’=M · ν. Вершини завжди мають чотири координати (x, y, z, w), хоча у більшості випадків координата w дорівнює 1, а для двовимірних даних координата z дорівнює 0. Слід звернути увагу, що перетворення виду і моделі також автоматично застосовуються до векторів нормалей до поверхні.
Задані перетворення виду та моделі комбінуються для створення матриці видового перетворення (view model matrix), що застосовується до координат об’єктів, які надходять під час їх побудови, для отримання видових координат. Надалі, якщо задано додаткові площини відсікання, вони будуть використані для вилучення певних об’єктів зі сцени або для отримання перерізу об’єктів.
Після цього OpenGL застосовує матрицю проекцій для отримання координат відсікання (clip coordinates). Це перетворення визначає відображуваний об’єм; об’єкти за його межами відсікаються і, таким чином не відображуються у кінцевій сцені. Наступним кроком виконується перспективний поділ (perspective division), під час якого усі значення координат поділяються на w для створення нормалізованих координат пристрою (normalized device coordinates). Нарешті, перетворені координати конвертуються у віконні координати (window coordinates) за допомогою перетворення порту перегляду. Розміри порту перегляду можна змінювати, отримуючи збільшене, стиснуте або розтягнуте зображення.
12.5.2 Особливості систем координат OpenGL
Як вже зазначувалося, у OpenGL вершини завжди задаються чотирма координатами. Це пов’язано [5] з використанням однорідних координат, що надають можливість подання усіх видів координатних перетворень у єдиній формі. В однорідній системі координат положення точки P(x, y, z) записується у вигляді P(W· x, W· y, W· z) або P(X, Y, Z, W) для будь-якого масштабного множника, причому тривимірні координати легко визначаються у вигляді:
x = X / W; y = Y / W; z = Z / W.
Таким чином звичайна ортогональна система координат отримується у вигляді проекції однорідної системи на площину W=1.
У матричній формі для позначення координат точки у певному тривимірному просторі з використанням однорідних координат застосовується запис [X Y Z W].
Перетворення однорідних координат записуються співвідношеннями:
 та
та 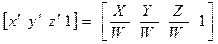 ,
,
де T – матриця перетворення.
Зокрема, такі перетворення координат, як x’ = x + l; y’ = y + m; z’ = z + n, можна записати у такій матричній формі:
 або
або 
Якщо ж розглядати тривимірне змінення масштабу – x”= x · a; y”= y · e; z’ = z · j, можна отримати такі матричні перетворення:
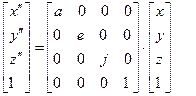
Перетворення, пов’язані з переміщеннями та масштабуванням, можна об’єднати у єдину матричну форму:
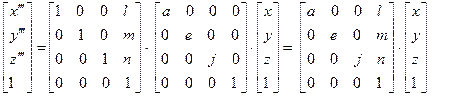
Узагальнена матриця перетворень тривимірних координат розміру 4 x 4 має вигляд:
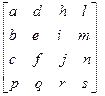 , при цьому підматриця
, при цьому підматриця 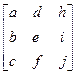 здійснює лінійні перетворення – зміну масштабу, зсув та обертання. Вектор
здійснює лінійні перетворення – зміну масштабу, зсув та обертання. Вектор 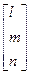 здійснює паралельне перенесення, вектор
здійснює паралельне перенесення, вектор 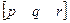 здійснює перспективне перетворення, а останній скалярний елемент s – загальну зміну масштабу.
здійснює перспективне перетворення, а останній скалярний елемент s – загальну зміну масштабу.
Повне перетворення, отримане шляхом впливу 4x4-матриці на вектор положення та нормалізації отриманого вектора називають білінійним перетворенням [5].
12.5.3 Перетворення координат
У OpenGL передбачається існування 4-х типів матриці – видових, проекційних та текстурних.
Будь-яка матриця може бути встановлена як поточна за допомогою команди glMatrixMode():
void glMatrixMode(GLenum mode);
|
|
