Граничные условия

До сих пор стыдливо замалчивался вопрос о реализации граничных условий (кроме простейших случаев). Пришла пора сказать о них несколько слов. Но сначала совсем чуть-чуть о том, откуда берутся эти самые граничные условия.

В редких случаях граничные условия можно получить из нехитрых физических соображений. Например, известно, что сквозь стенку поток массы равен нулю. Поток массы равен сумме потоков ионов и нейтральных частиц (массой электронов пренебрегают). Отсюда легко и просто записывается соответствующее граничное условие[15]:

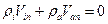
Гораздо чаще для получения граничного условия решается задача о нахождении параметров в пристеночном слое. Для этого решаются те же самые уравнения магнитной гидродинамики (или даже Больцмана)[16]. Как правило, достаточно решить одномерную задачу (если толщина пристеночного слоя много меньше характерного размера конечной задачи). Иногда удается получить аналитическое решение. Чаще численное решение аппроксимируется какой-то простой формулой. Результат используется в качестве граничного условия для «большой» задачи.

Но бывает, что ситуация совсем плохая, и никакой признанной теории нет. Тогда граничное условие выписывается на основе экспериментальных данных. Такое очень часто случается для взаимодействия разреженной плазмы со стенкой. Описание таких процессов как эмиссия электронов, распыление материала стенки, углы под которыми частицы покидают стенку – основывается на экспериментальных данных.

Ранее отмечалось, что с точки зрения математики при моделировании плазмы используются три типа граничных условий:

1) условие Дирихле. На границе задается значение функции.

2) Условие Неймана. На границе задается значение производной функции. Часто применяется для параболических и эллиптических уравнений.

3) Смешанное. На границе задается линейная комбинация условий Дирихле и Неймана.

Здесь подробно рассмотрим первые два типа условий. Третий тип встречается гораздо реже и реализуется аналогично.

В одномерном случае всегда можно расположить узел расчетной сетки точно на границе. В связи с этим, не возникает ни каких проблем с условием Дирихле: просто в узле сетки значение функции принимается равным значению из граничного условия. Для условия Неймана уже наблюдается некоторое разнообразие. Рассмотрим левую границу расчетной области. Индекс узла, лежащего на границе будем считать нулевым.

Условие Неймана записывается в виде

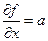
Простейший разностный аналог этого условия будет

Но если для решения уравнений используются схемы второго порядка, то желательно и граничное условие аппроксимировать со вторым порядком. Этого можно добиться двумя способами. Способ первый: использовать для граничного условия соотношение:

при этом производные тоже должны быть аппроксимированы разностями второго порядка точности. Получаем

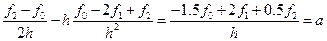
Второй способ основан на использовании фиктивного узла. За пределами расчетной области «создают» еще один узел, значение в котором не будет использоваться в окончательных результатах. Но, для внутреннего употребления, функции в этом узле приписывается какое-то значение. Для описания граничного условия используется центральная разность

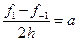
Для узла, соответствующего границе, решается тот же разностный аналог исходного уравнения, что и для узлов, расположенных в плазме. Но в этом разностном соотношении используется значение в фиктивном узле, полученное по приведенной выше формуле.

В двумерном и трехмерном случаях не всегда выгодно располагать узлы сетки ровно на границе плазмы[17]. Естественно, существуют разные способы решения этой проблемы. Первый способ основан на тех же самых фиктивных узлах. При этом сетка, по-прежнему, остается регулярной.

Условие Дирихле

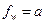
записывается (для аппроксимации первого порядка) довольно просто

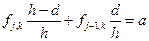
для аппроксимации второго порядка чуть посложнее

Условие Неймана обычно записывается в виде

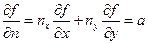
где n_x и n_y – компоненты вектора нормали к поверхности. Аппроксимация первого порядка для этого условия может быть, например, такой

аппроксимация второго порядка будет выглядеть так

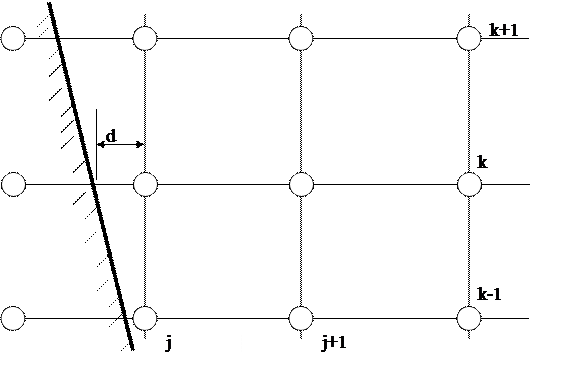
Однако, для сложной геометрии этот способ не всегда применим. Он предполагает, что каждому пересечению линии сетки с границей соответствует один фиктивный узел. Но так бывает не всегда (см. Рис.). Узел, которому соответствуют два условия, выделен черным цветом.

Рассмотрим способ, лишенный такого недостатка. За избавление от недостатка пришлось заплатить усложнением алгоритма. В данном способе отказываются от фиктивных узлов (а следовательно и от регулярности сетки) и ставят узлы на пересечение линий сетки с границей. Это значительно облегчает реализацию условия Дирихле. Но формулы для условия Неймана получаются довольно громоздкие (к тому же нужно рассмотреть несколько вариантов для различных случаев пересечения границей). Формулы, конечно же, получаются из того же самого разложения функции в ряд Тейлора. Но в большинстве книг (ссылаясь на элементарность этой процедуры) их не приводят. Я тоже поленился приводить их здесь: места занимают много, а к пониманию процесса ничего не добавляют. Ограничусь картинкой для этого метода. Вот она.

Теперь изучивший вышеизложенное должен уметь решать задачи, по крайней мере, одним методом.