
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Аппроксимация
|
|
Итак, требуется заменить имеющиеся уравнения их дискретными аналогами. Такой процесс называется дискретизацией уравнений. Рассмотрим производные по x (производные по другим переменным записываются совершенно аналогично). Отсортируем дискретные значения переменной x по возрастанию и проиндексируем их. Значения производных в узле сетки приближенно записываются (аппроксимируются) через значения функции в данном и ближайших узлах. Обязательное условие: приближенное значение производной, посчитанное по дискретному аналогу, должно стремиться к точному значению при стремлении расстояния между узлами к нулю. Минимальное количество точек, необходимое для аппроксимации n-й производной, равно n+1. Так, первую производную можно приближенно найти, зная значение функции в 2 точках, вторую производную – в 3 точках.
Самым распространенным способом дискретизации является разложение функции в ряд Тейлора. При выводе дискретного аналога производной используются только несколько первых членов ряда (остальные полагаются равными нулю). Порядком аппроксимации называется порядок последней учитывающейся производной в ряде Тейлора[8]. Рассмотрим простейшую аппроксимацию первой производной. В точке с номером j ее можно получить двумя способами.
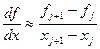

Первая из этих формул называется аппроксимацией разностью вперед, вторая – аппроксимацией разностью назад. Это формулы первого порядка. Попробуем написать формулу второго порядка.
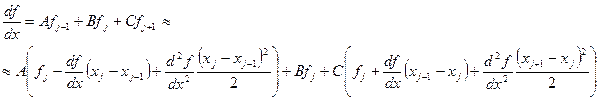
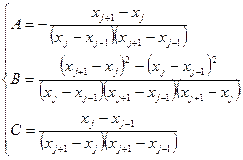
Для равномерных сеток (xj+1-xj)=(xj-xj-1). Обычно шаг сетки при этом обозначают через h. При этом запись дискретного аналога первой производной существенно упрощается

В этом случае принято говорить, что первая производная аппроксимируется центральной разностью. Аналогично записываются дискретные аналоги для второй производной.
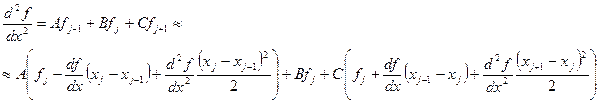
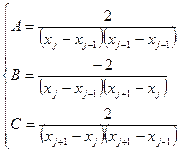
Для равномерной сетки получаем
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
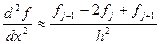
Далее, чтобы избежать громоздких выражений, будем рассматривать только равномерные сетки.
При записи дискретного аналога дифференциальных уравнений возникает уже гораздо большее разнообразие вариантов. Рассмотрим волновое дифференциальное уравнение первого порядка.

Оно описывает распространение волны (перенос массы или заряда) со скоростью a. Как указывалось выше к таким уравнениям можно свести гиперболические уравнения. Будем рассматривать именно такой случай. Считаем, что мы идем маршевым методом по времени. Нам известно распределение функции по x в некоторый момент времени и нужно найти распределение в следующий момент. Рассмотрим аппроксимации первого порядка. Значения функции в узлах сетки будем обозначать f, jk, где первый индекс относится к значению времени, а второй – координаты. Производную по времени аппроксимируем выражением
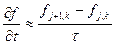
где t - шаг по времени. А производную по координате можно аппроксимировать как разностями вперед, так и разностями назад. Получаем первые две возможные аппроксимации.
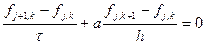
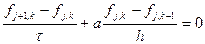
Для наглядности часто рисуют графические изображения разностных схем, называемые шаблонами. Приведем шаблоны двух описанных формул. На рисунках считается, что координата x идет горизонтально слева направо, а ось y направлена вертикально снизу вверх.

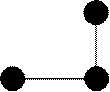
Строгих стандартов на шаблоны не существует. Например, часто рисуют стрелки из узлов, где значения известны, в узел (узлы), где значения неизвестны. Часто в одной книге шаблоны нарисованы в разных местах в разных стилях. Здесь, тоже не будем придерживаться одного стиля.
За приведенные графические изображения рассмотренные схемы часто называют «правый уголок» и «левый уголок». В обеих этих схемах на новом (по времени) слое используется лишь один узел, следовательно, значение в этом узле можно явным образом выразить через значения в других узлах.

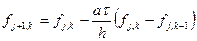
Такие схемы называются явными. Зная значения на j-м слое, легко получаются значения на j+1-м слое. Если производную по координате выписать на новом слое, то получим две неявные схемы.
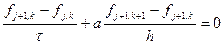
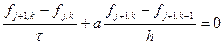
Они имеют следующие шаблоны
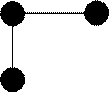
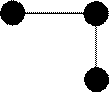
В случае неявной схемы мы получаем не конечную формулу для значения функции в узле, а связи между неизвестными значениями в узлах на новом слое. Перебрав все значения индекса k мы получаем систему (линейных) алгебраических уравнений, которую надо решить для получения искомых значений. В рассматриваемом случае можно отделаться малой кровью. Каждое уравнение будет связывать два соседних узла. Найдя значение в каком-либо узле на новом слое, легко получить значение в соседнем. Далее, двигаясь по цепочке, получаем значения во всех узлах на новом слое. Таким образом, нужно знать хотя бы одно значение. Его можно взять из граничного условия. В общем случае в неявных схемах без специальных ухищрений не удается обойтись без решения системы уравнений.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Посмотрим, что мы реально считаем методом конечных разностей. Выберем схему «правый уголок». Разложим искомую функцию в ряд Тейлора в окрестности точки с индаксами j и k и учтем члены со второй производной. Итак, имеем
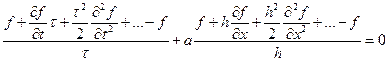
после сокращения получаем, то, что решаем реально
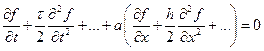
То есть, дискретизация привела к тому, что, надеясь решить одно уравнение, получаем решение другого уравнения. Радует лишь то, что с уменьшением шагов по времени и по пространству разница между уравнениями уменьшается. Тем не менее, при любых ненулевых шагах реально решаемое уравнение может не только иметь иные (по сравнению с исходным) свойства, но даже принадлежать к другому типу. Например, исходное рассматриваемое уравнение предполагает, что волна движется в пространстве не меняя своей формы. Для демонстрации зададим в качестве начального распределения разрывное распределение (см. случай а на рисунке ниже). Если неудачно выбрана расчетная схема или ее параметры, то можно получить решения, показанные на том же рисунке с обозначениями б и в, или вообще не получить никакого разумного решения.
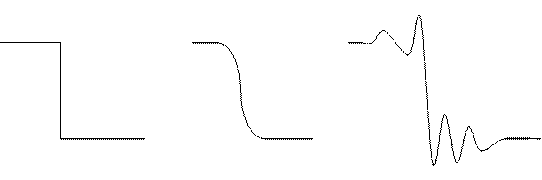
а б в
Теперь рассмотрим параболическое уравнение, а именно цветовое уравнение
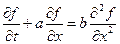
(Как отмечалось выше, такое название оно получило за то, что описывает, в том числе, распространение подкрашенной жидкости в воде.) Параметр a определяет скорость конвективного переноса концентрации (или, например, температуры), а параметр b определяет диффузию (теплопередачу). Выберем явную схему. Первую производную по пространству для начала аппроксимируем с помощью правой разности. Получаем дискретный аналог дифференциального уравнения
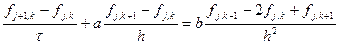
Как и раньше разложим функцию в ряд Тейлора, но по пространству учтем третью производную.
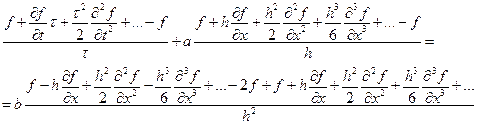
после сокращений получаем

теперь сгруппируем вторые производные по x. Получим
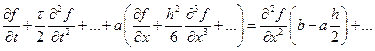
То есть получается, что мы не только решаем другое уравнение, но и коэффициенты в нем другие. Коэффициент b имеет физический смысл коэффициента диффузии (теплопроводности, вязкости) и не может быть отрицательным. А у нас получилось, что при 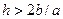 коэффициент диффузии становится отрицательным, что не соответствует никакой физике. Добавку к коэффициенту диффузии (теплопроводности, вязкости) принято называть сеточной (или схемной) диффузией (теплопроводностью, вязкостью).
коэффициент диффузии становится отрицательным, что не соответствует никакой физике. Добавку к коэффициенту диффузии (теплопроводности, вязкости) принято называть сеточной (или схемной) диффузией (теплопроводностью, вязкостью).
Теперь рассмотрим случай, когда первая производная аппроксимируется центральной разностью. Получаем дискретный аналог дифференциального уравнения

Как и раньше разложим функцию в ряд Тейлора, но по пространству учтем третью производную.
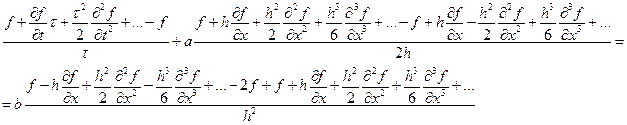
после сокращений получаем
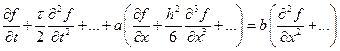
По сравнению с исходным уравнением присутствуют член, пропорциональный первой степени шага по времени, и член, пропорциональный второй степени шага по пространству. В таком случае говорят, что данная схема имеет второй порядок аппроксимации по простронству и первый – по времени. В целом, когда говорят о порядке аппроксимации уравнения, под порядком понимают наименьший из порядков аппроксимации по всем переменным. В данном случае мы имеем аппроксимацию первого порядка.
Для линейных уравнений есть «точные» оценки погрешности расчета. Но при моделировании плазмы, как правило, приходится иметь дело с нелинейными уравнениями. Для них точных оценок нет. Для оценки точности расчета обычно проводят два (иногда больше) расчета на разных сетках. Если на второй сетке шаги по всем переменным вдвое меньше, чем на первой, и схема имеет первый порядок аппроксимации, то погрешность уменьшится примерно вдвое. «Примерно» потому, что в разложении в ряд Тейлора существуют члены с производными более высоких порядков и, соответственно, с более высокими степенями шагов. Таким образом, разница между результатами расчетов будет примерно соответствовать погрешности расчета с более мелкой сеткой. Если использовалась аппроксимация второго порядка, то уменьшение шагов вдвое приводит к уменьшению погрешности примерно в четыре раза.
Следует отметить, что для таких оценок необходимо пропорционально изменять и шаг по времени и шаг по пространству. Если уменьшать только один из шагов, оставляя другой без изменения, то погрешность может как увеличиваться, так и возрастать. Объясняется это тем, что погрешность зависит и от соотношения шагов. Для того, чтобы это наглядно показать, составим дифференциальное приближение волнового уравнения первого порядка. От проделанных выше операций эта процедура отличается исключением высших производных по времени из реально решаемых уравнений. Итак, рассматриваем уравнение
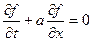
используя следующую разностную схему
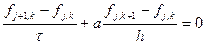 .
.
Для этого случая мы ранее уже получили выражение
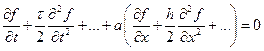 .
.
Чтобы выразить вторую производную по времени через производные по пространству продифференцируем исходное уравнение по времени. Получаем
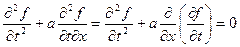 .
.
Выразим первую производную по времени через исходное уравнение
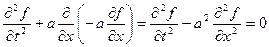
Теперь реально решаемое уравнение можно записать в виде
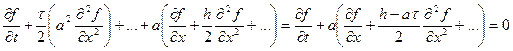 .
.
Полученный результат называется дифференциальным приближением рассматриваемой разностной схемы. Из него видно, что наименьшую погрешность можно получить, задав шаги, связанные соотношением
h=aτ.
Как показано выше, члены, отвечающие за погрешность в реально решаемых уравнениях, пропорциональны некоторым производным от искомой функции. Но в природе, в том числе и в плазме, могут существовать области с очень большими градиентами. Часто проще их описать разрывными функциями. Значения производных в этих областях очень велики (для разрывов – бесконечны), следовательно, и погрешность численного решения может быть недопустимо большой. Простого универсального метода обхода этой неприятности для произвольной системы дифференциальных уравнений нет. Но для уравнений магнито-гидродинамики такой способ есть. Рассмотрим две эквивалентные записи уравнения, описывающего перенос массы (или заряда) вдоль оси
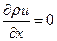
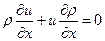
Будем считать, что распределение плотности вдоль оси нам известно. Причем плотность задана разрывной функцией
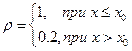
Пусть x0> 0, u(0)=1. Очевидно, что аналитическое решение для скорости будет

Попробуем решить уравнение во второй форме записи методом конечных разностей. Распишем разностную схему
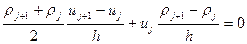
Выразим значение скорости в следующей точке через значение в предыдущей
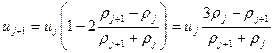
Получаем, что при переходе через разрыв скорость получит новое значение 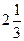 . То есть расход массы (заряда) снизился примерно вдвое. Причем этот результат не зависит от шага сетки. Если мы используем первую форму записи уравнения, то схема записывается
. То есть расход массы (заряда) снизился примерно вдвое. Причем этот результат не зависит от шага сетки. Если мы используем первую форму записи уравнения, то схема записывается
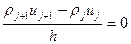
скорость в следующей точке равна
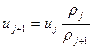
При переходе через разрыв получаем точное решение. Чтобы избежать подобных проблем исходные уравнения, по возможности, нужно приводить к виду
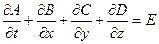
То есть без коэффициентов перед производными. Такой вид называется дивиргентным. Иногда говорят о дивиргентной форме записи уравнения. Если в уравнениях магнто-гидродинамики не учитываются вязкость, диффузия и теплопроводность (т.е. процессы, при записи которых используются вторые производные), то их можно привести к дивиргентному виду. Рассмотрим правые части уравнения сохранения массы и одного из уравнений сохранения импульса
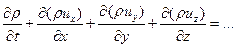
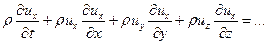
первое из них уже в дивиргентной форме. А второе можно привести к дивиргентному виду если прибавить к нему первое уравнение умноженное на ux. Тогда получаем
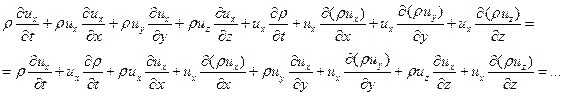
Окончательно уравнение импульса переписывается в виде
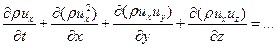
|
|
