
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Регресійний аналіз
|
|
ОЗНАЧЕННЯ 6.1. Математичний метод, що забезпечує таку підгонку вибраної кривої, при якій експериментальні точки лягають на неї щонайкраще в сенсі критерію найменших квадратів, називається регресійним аналізом.
Загальний вигляд кривої найкращого наближення аналітик повинен вибрати за результатами вивчення діаграми розкиду. Використовуваний надалі математичний апарат повинен забезпечувати найкраще наближення кривої до експериментальних даних незалежно від того, наскільки добре вибраний тип кривої. Під наближенням кривої до експериментальних даних розуміється лише процес обчислення значень констант або параметрів таким чином, щоб сума квадратичних відхилень була мінімальною. Аналітик повинен заздалегідь вибрати найкраще апроксимуюче рівняння.
Детальний опис методів регресійного аналізу можна знайти у спеціальній літературі (наприклад, [3]). В даній лекції обмежимося обговоренням простого випадку, коли очікується, що 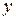 є лінійною функцією однієї змінної
є лінійною функцією однієї змінної  .
.
Основна модель лінійного співвідношення між залежною змінною 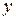 і незалежною змінною
і незалежною змінною  дається рівнянням
дається рівнянням
 , (6.1)
, (6.1)
де  — початкове значення
— початкове значення 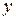 ;
;
 - тангенс кута нахилу прямої;
- тангенс кута нахилу прямої;
 - випадкова похибка.
- випадкова похибка.
Величини  ,
, 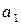 і
і  невідомі. Якщо ми маємо сукупність даних, що складається з відповідних значень
невідомі. Якщо ми маємо сукупність даних, що складається з відповідних значень  і
і 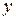 , оцінки
, оцінки 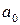 і
і  необхідно отримати з цих даних. Для цього скористуємося наступними рівняннями:
необхідно отримати з цих даних. Для цього скористуємося наступними рівняннями:
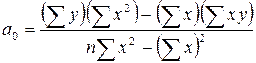 , (6.2)
, (6.2)
 . (6.3)
. (6.3)
ПРИКЛАД 6.1. Нехай маємо чотири експериментальні крапки (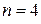 ) і хочемо отримати лінійну апроксимацію цієї сукупності даних. Відповідні обчислення наведено в таблиці 6.1.
) і хочемо отримати лінійну апроксимацію цієї сукупності даних. Відповідні обчислення наведено в таблиці 6.1.
Таблиця 6.1.
| x | y | x2 | xy | |
| Суммы |
У відповідності з (6.2) та (6.3) маємо
 ,
,
 .
.
Виходячи з цього, рівняння регресії буде мати вигляд
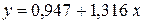 .
.
|
|
