Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Підбір апроксимуючих кривих

Лекція 6.

Попередня обробка емпіричних даних.

Підбір апроксимуючих кривих. Регресійний аналіз. Кореляція.

Підбір апроксимуючих кривих

У багатьох технічних системах має місце функціональний зв'язок між двома або більш змінними, і бажано цей зв'язок виявити. Інколи це буває просто, оскільки зв'язок легко виявляється або відомий заздалегідь; проте набагато частіше функціональ­ний зв'язок надзвичайно складний або абсолютно не відомий. У останньому випадку можна зіткнутися з необхідністю ввести деяку гіпотезу про характер функціональної залежності, тобто апроксимувати її деяким відносно простим мате­матичним виразом, наприклад лінійним співвідношенням або многочленом. Для пошуку таких математичних функціональних або структурних залежностей між двома або більш змінними за накопиченими експериментальними даними вельми корисні методи регресійного і кореляційного аналізу. Регресійний аналіз дає можливість побудувати, виходячи з сукупності експериментальних даних, що маються, рівняння, вигляд якого задає аналітик, а кореляційний аналіз дозволяє су­дити про те, наскільки добре експериментальні точки узгоджуються з вибраним рівнянням («лягають» на відповідну криву).

Першим кроком при виведенні рівняння, що апроксимує необхідну залежність, є збір даних, що відображають відповідні значення змінних. Хай, на­приклад, передбачається, що вихід хімічного процесу є функцією кількості каталізатору, що вводиться в реактор. Позначимо через 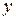величину виходу продукту і через кількість каталізатора, що вводиться. 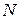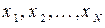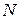Тоді з даних, що раніше реєструвалися, або отриманих в результаті спеціального експерименту, мож­на узяти вибірку об'ємом значень і відповідних значень

Наступним кроком буде нанесення цих точок 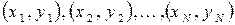на графік в прямокутній системі координат. В ре­зультаті ми отримаємо так звану діаграму розкиду, з якої часто удається чисто візуальним способом знайти плавну криву, що апроксимує функціональну залежність. На­приклад, з графіка на рис. 6.1 видно, що експериментальні точ­ки добре лягають на пряму лінію. В той же час точки, нанесені на рис. 6.2, мабуть, краще лягають на деяку іншу криву.

Задача знаходження для апроксимуючих кривих таких рівнянь, які щонайкраще відображують дану сукуп­ність експериментальних точок, умовно називається задачею під­гонки кривих по точках. Перш за все аналітик повинен вибрати вигляд кривої, для якої він шукатиме апроксимуюче рівняння. Нижче наводиться для довідок декілька найбільш поширених видів

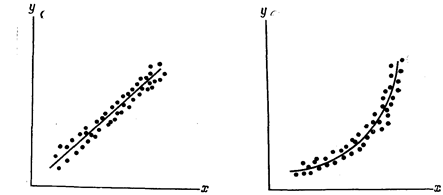
Рис. 6.1 Рис. 6.2

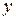апроксимуючих кривих і відповідних ним рівнянь ( —незалежна змінна; —залежна змінна; інші букви та цифри відносяться до констант або до параметрів кривих):

1) — пряма лінія;

2) 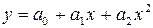— квадратна парабола;

3) 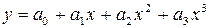— кубічна парабола;

4) — парабола четвертого ступня;

5) 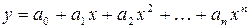— парабола n -го ступня;

6) 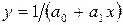, або — гіпербола;

7) 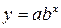, або 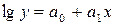— експонента;

8) 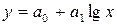— логарифмічна крива;

9) 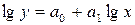— кубічна логарифмічна крива

Зрозуміло, можуть знайти застосування, і криві багатьох інших видів. Аби вирішити, яку апроксимацію використовувати, необхідно вивчити діаграму розкиду і порівняти її форму з формою декількох кривих, відповідних різним рівнянням; форми деяких з них показані на рис. 6.3. Інколи буває корисно також досліджувати діаграму розкиду, перетворивши змінні. Для цього можна скористатися спеціальною логарифмічною сіткою, на якій відповідно масштаб по одній або обох осях координат вибраний ло­гарифмічним. При цьому, наприклад, якщо діаграма розкиду у системі координат 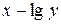виявляється лінійною, слід скористатися рівнянням експоненти. Подібним же чином, якщо діаграма лінійна в масштабі , слід узяти апроксимуюче рівняння кубічної логарифмі­чної кривої.

Перш ніж йти далі, визначимо, що слід розуміти під «найкращою» підгонкою кривої. Перш за все спробуємо просто покластися на наш здоровий глузд. Накладемо на діаграму розкиду лекало або гнучку лінійку і спробуємо провести кри­ву так, щоб вона проходила «посередині», тобто аби всі точ­ки, що не попали на криву, були від неї на однаковій міні­мальній відстані. Недолік цього способу полягає в тому, що кожен аналітик отримуватиме свої власні криві і рівняння, що апроксимують їх. Тому хотілося б виробити такий критерій «найкращого наближення», який був би об'єктивний, відповідав інтуїтивному поняттю прийнятного і мав порівняно просте математичне представлення.

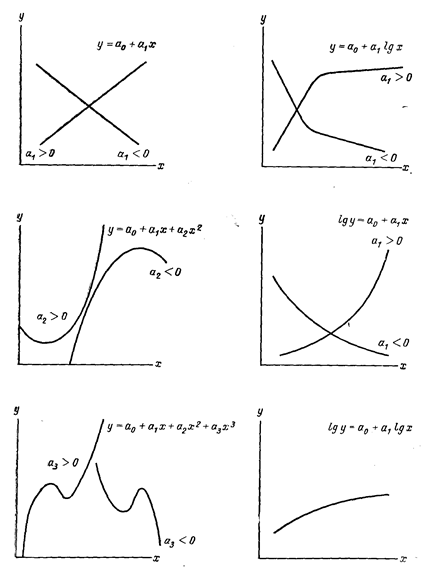
Рис. 6.3

Різні види апроксимуючих кривих

Для вирішення цієї задачі найчастіше використовується відомий [2, 3] метод най­менших квадратів, який, по суті, просто формалізує процедуру підбору апроксимуючої кривої на око, коли ми прагнемо звести до мінімуму відхилення експериментальних то­чок від підібраної кривої. Пояснимо це прикладом. На рис. 6.4, де через 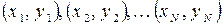позначені координати екс­периментальних точок, для будь-якого заданого , скажемо 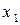, матиме місце різниця між 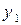і відповідним значенням, що одержується по теоретичній кривій. Позначимо цю різницю символом 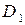і називатимемо її відхиленням. Це відхилення може бути позитивним, негативним або нульовим. Відповідно для кожної з експериментальних точок можна обчис­лити значення відхилень . Тоді в якості міри на­ближення кривої до експериментальних даних можна рахувати суму абсолютних відхилень, тобто 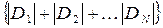. Оскільки відхилення можуть бути позитивними або негативними, з математичної точки зору простіше звести їх значення в квадрат і надалі мати справу з квадратичними відхиленнями. Сума останніх, вочевидь, дасть таку ж хорошу міру якості наближення. Тому вважатимемо, що зі всіх можливих апроксимуючих кривих кривої найкращого наближення для даної сукупності експериментальних точок буде та, для якої сума мінімальна. Так чином визначається критерій найкращого наближення за методом найменших квадратів.

Рис. 6.4