
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Рівняння Топена і рекурентні співвідношення.
|
|
Введемо величину r(z), яку визначимо наступним чином:
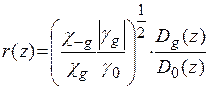 (1.41)
(1.41)
Нескладно побачити, що визначена нами таким чином функція r(z) при z=0 рівна комплексному коефіцієнту відбивання (ККО) в асиметричній геометрії Брега. Нагадаємо, що в геометрії Брега завжди 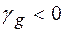 , так, що
, так, що 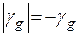 .Згідно (1.41) маємо:
.Згідно (1.41) маємо:
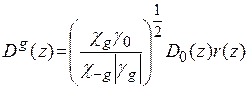 . (1.42)
. (1.42)
Із першого рівняння системи (1.38) після деяких перетворень отримаємо:
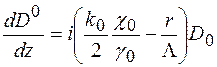 , (1.43)
, (1.43)
де 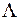 - екстинкція – (1.27в).
- екстинкція – (1.27в).
При отриманні рівняння (1.43) для прозорого кристалу повинно бути використане наступне правило вибору знаків:
 .
.
Підставляючи в друге рівняння системи (1.38) замість 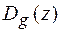 (1.42), і проводячи необхідні перетворення і замінюючи похідну
(1.42), і проводячи необхідні перетворення і замінюючи похідну 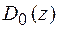 правою частиною рівняння (1.43), отримаємо диференціальне рівняння першого порядку для ККВ:
правою частиною рівняння (1.43), отримаємо диференціальне рівняння першого порядку для ККВ:
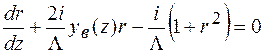 . (1.44)
. (1.44)
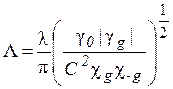
Рівняння (1.44) називається рівнянням Топена. При записі (1.44) введені наступні позначення:
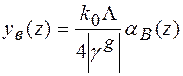 , (1.45)
, (1.45)
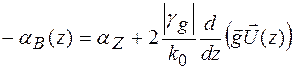 , (1.46)
, (1.46)
де 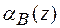 - локальна Брегівська аккомодація – (1.39), параметр
- локальна Брегівська аккомодація – (1.39), параметр 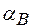 - визначений в(1.27а), а
- визначений в(1.27а), а 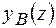 - при нехтовно малому поглинанні має зміст нормованої локальної кутової відстройки від невиправленого на заломлення кута Брега
- при нехтовно малому поглинанні має зміст нормованої локальної кутової відстройки від невиправленого на заломлення кута Брега 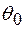 (1.27а).
(1.27а).
Рівняння (1.27) відноситься до рівнянь типу Ріккаті. Для його рішення слід задати одну граничну умову на вихідній поверхні z=t. Ця умова описує відбивні властивості середовища, яке знаходиться поза досліджуваним кристалом. Якщо поза кристалом вакуум то r(t)=0, якщо ж поза ним знаходиться другий кристал то з ККВ r2(t), то гранична умова при z=t має вигляд r(t)=r2(t). Оскільки гранична умова задається на нижній поверхні кристалу, то і рішення рівняння Топена (1.44) ведеться знизу.
Для півбезмежного кристалу без спотворень (U(z)=0) диференціальне рівняння стає алгебраїчним, тобто:
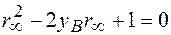

Оскільки в цьому випадку відношення 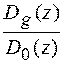 не залежить від координати z. Останнє твердження базується на тому, що добавка чи забирання шару довільної товщини змінює ККВ напівбезмежного кристалу
не залежить від координати z. Останнє твердження базується на тому, що добавка чи забирання шару довільної товщини змінює ККВ напівбезмежного кристалу 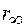 . Звідси знайдемо ККВ
. Звідси знайдемо ККВ 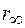 :
:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
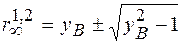 . (1.47)
. (1.47)
Тут вибір знаків перед коренем виконується на основі наступних умов:
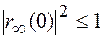 i
i 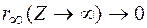 при
при 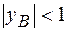 .
.
В кристалі з поглинанням слід зберігати лише знак плюс (+) в (1.47) і використати значення кореня з додатною уявною частиною.
При брегівській дифракції на досконалому кристалі кінцевої товщини рівняння (1.44) слід розв'язувати, замінюючи 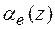 (1.45б) на
(1.45б) на 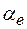 (1.27а) з однією граничною умовою r(t)=0, що задається на нижній грані кристалу. У випадку кінематичного розсіяння ККВ за модулем |r|< 1, тому складовою r2 в рівнянні (1.44) можна знехтувати, так що в кінематичному наближенні рівняння Топена стає лінійним
(1.27а) з однією граничною умовою r(t)=0, що задається на нижній грані кристалу. У випадку кінематичного розсіяння ККВ за модулем |r|< 1, тому складовою r2 в рівнянні (1.44) можна знехтувати, так що в кінематичному наближенні рівняння Топена стає лінійним
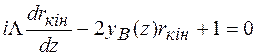 . (1.48а)
. (1.48а)
Загальне рішення рівняння (1.48а) для довільної функції 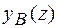 , що задовільняє умові
, що задовільняє умові 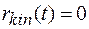 має вигляд
має вигляд
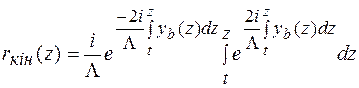 (1.48б)
(1.48б)
На поверхні z=0 цей результат можна переписати так
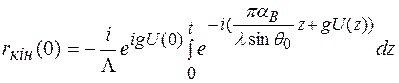 ,
,
де аккомодація 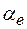 визначена в (1.46). В кінематичному наближенні ефекти заломлення не суттєві із-за великих ширин КДВ, тому
визначена в (1.46). В кінематичному наближенні ефекти заломлення не суттєві із-за великих ширин КДВ, тому 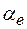 можна поміняти на a. Якщо зміщення відраховуються від вхідної поверхні, то U(0)=0. Для врахування аморфізації в показник експоненти під інтегралом слід ввести W(z). Це рішення, наприклад, у випадку симетричної брегівської дифракції від ідеального тонкого (t< < lext) кристалу переходить заміною yB(z) на yB з врахуванням визначення (1.41) у відомий результат елементарної кінематичної теорії дифракції
можна поміняти на a. Якщо зміщення відраховуються від вхідної поверхні, то U(0)=0. Для врахування аморфізації в показник експоненти під інтегралом слід ввести W(z). Це рішення, наприклад, у випадку симетричної брегівської дифракції від ідеального тонкого (t< < lext) кристалу переходить заміною yB(z) на yB з врахуванням визначення (1.41) у відомий результат елементарної кінематичної теорії дифракції
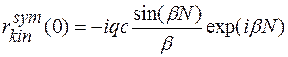 ,
, 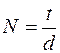 ,
, 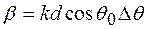 .
.
Особливий інтерес для окремих випадків представляє задача дифракції на одномірноспотвореному кристалі товщини t, розміщеному на напівбезмежній досконалій підкладці із близьким значенням параметра гратки. Для зручності введемо ККВ 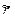 , тобто:
, тобто:
 .
.
Тоді згідно (1.44), отримаємо
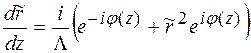 , (1.44')
, (1.44')
де 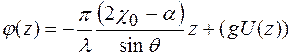 . Гранична умова для рівняння (1.44) має вигляд
. Гранична умова для рівняння (1.44) має вигляд 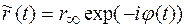 , де
, де 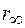 - ККВ від досконалої напівбезмежної підкладинки (1.47). Вважатимемо, що спотворений шар має слабку відбивну здатність (кінематичне наближення). В силу цього допущення в правій частині рівняння (1.44') в другій складовій множник
- ККВ від досконалої напівбезмежної підкладинки (1.47). Вважатимемо, що спотворений шар має слабку відбивну здатність (кінематичне наближення). В силу цього допущення в правій частині рівняння (1.44') в другій складовій множник 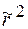 можна замінити множником
можна замінити множником 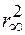 . В результаті отримаємо лінійне рівняння першого порядку із відомою правою частиною. Інтегрування цього рівняння з наступним переходом від
. В результаті отримаємо лінійне рівняння першого порядку із відомою правою частиною. Інтегрування цього рівняння з наступним переходом від 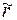 до
до 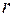 дає наступний результат для ККВ двохшарової структури на поверхні z=0:
дає наступний результат для ККВ двохшарової структури на поверхні z=0:
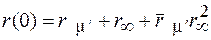 , (1.48в)
, (1.48в)
де ККВ спотвореного шару 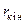 визначений співвідношенням (1.48в), а
визначений співвідношенням (1.48в), а 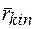 - ККВ від оберненої сторони спотвореного шару.
- ККВ від оберненої сторони спотвореного шару.
Зауважимо, що остання складова виразу (1.48в) дає помітний вклад в розсіяння тільки поблизу області повного відбивання, де 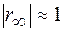 . Для знаходження наступного наближення розв'язку лінеаризованого рівняння (1.44) ітераційну процедуру можна було б продовжити, використовуючи вираз для r(0) (1.48в) в якості першого наближення.
. Для знаходження наступного наближення розв'язку лінеаризованого рівняння (1.44) ітераційну процедуру можна було б продовжити, використовуючи вираз для r(0) (1.48в) в якості першого наближення.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Взагалі ж аналітичне рішення рівняння Топена (1.44) є не менш складне ніж рішення вихідної системи (1.38) або (1.40), і в цьому розумінні перехід до нього не дає ніяких переваг. Проте, воно є зручним при чисельному розв’язку задач дифракції в кристалах із спотвореннями оскільки розв’язок одного рівняння першого порядку (1.44) із однією граничною умовою є суттєво простішим розв’язку вихідної системи (1.38) із граничними умовами заданими на різних поверхнях кристалу. Зауважимо, що рівняння типу (1.44) добре дослідженні в радіофізиці при дослідженні розповсюдження сигналів в шаруватих середовищах.
|
|
