Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Двійкова арифметика

У цифрових та мікропроцесорних пристроях над двійковими числами виконуються як логічні, так і арифметичні операції. Арифметичні операції (додавання, віднімання, множення, ділення) над двійковими числами здійснюються (реалізуються) з допомогою спеціальних алгоритмів, які не використовуються у десятковій системі числення. У цих алгоритмах переважає операція додавання як додатних, так і від’ємних чисел, яку досить просто реалізувати.

Цифрові пристрої оперують тільки цілими і дійсними числами. Останні можуть бути подані з фіксованою або з плаваючою комою (точкою) [2; 4]. Незалежно від форм зображення знаки дійсних чисел “+” і “–” в ЦТ кодують цифрами – відповідно нулем (0) і одиницею (1). При цьому код знака двійкового числа розташовують перед старшим розрядом цього числа, кожний розряд якого має у розрядній сітці своє місце. Наприклад, потрібно перетворити десяткове число – 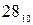у двійковий код і розмістити його в однобайтну розрядну сітку, один розряд якої відведений під код знака числа. Якщо при записі від’ємного числа знаковий розряд відокремлювати, наприклад, крапкою, маємо – .

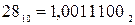Основною арифметичною операцією, яка використовується в цифрових пристроях для виконання різних обчислень, є операція алгебраїчного додавання двійкових чисел. Операція віднімання легко виконується через додавання, якщо змінити знак від’ємника на протилежний, а саме: 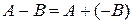. Операції множення і ділення також виконуються з допомогою операції додавання та деяких логічних дій при застосуванні зсуву часткових результатів ліворуч або праворуч [2; 4].

Зупинимось на операції додавання двійкових чисел.

Операція додавання в цифрових пристроях виконується порозрядно, починаючи з молодших розрядів доданків. При цьому в кожному одноіменному розряді доданків підсумовуються відповідні цифри та переноситься попередній розряд суми. Додавання молодших розрядів двійкових чисел здійснюється лише з двома доданками: 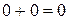; ; ; 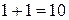, де у числі 10 цифра 1 – перенос у наступний, (старший) розряд.

Пристрій, що виконує операцію додавання двійкових чисел, називається суматором, а пристрій, що реалізує підсумовування молодших розрядів двійкового числа – напівсуматором. Порозрядне підсумовування двох чисел як суматор, так і напівсуматор виконують за модулем 2 згідно з правилом 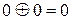; ; 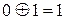; 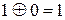, яке ще застосовують для порівняння двох чисел.

Виконання операції додавання додатних чисел, наприклад, 0, 0111 і 0, 0101. Для виконання операції додавання від’ємних чисел застосовуються спеціальні коди – обернений та доповняльний. Обернений код 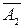від’ємного числа 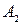отримується при інвертуванні всіх цифр у кожному розряді, тобто заміні нуля одиницею, одиниці нулем, а у знаковому розряді ставиться одиниця. Отже, обернений код числа 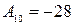буде 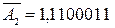. Якщо виконувати операцію , тобто зображати від’ємне число 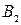оберненим кодом 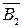, може виникнути одиниця, яку потрібно додати до молодшого розряду одержаної суми. Однак цю операцію, яка називається циклічним переносом, технічно реалізувати не вигідно, бо вона вимагає ще однієї операції додавання, що істотно збільшує час виконання дії. Тому для додавання від’ємних чисел перевага надається доповняльному коду числа 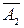, який утворюється від оберненого додаванням одиниці до його молодшого розряду. При цьому відпадає необхідність у циклічному переносі одиниці та ще одного додавання. У випадку переповнення у знаковому розряді одиниця переносу просто відкидається і не враховується. Тому всі від’ємні числа, які використовуються для виконання різних арифметичних дій, подають у доповняльному коді. 0тже, доповняльний код 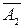від’ємного n-розрядного числа 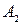одержується з оберненого 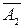як (у молодшому розряді), де 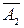=1, – від’ємне число в оберненому коді.

Якщо у знаковому розряді суми отримано одиницю, тобто результат від’ємний, значення отриманого числа є у доповняльному коді, а якщо нуль, результат додавання отримано у прямому коді. Сума доповняльних кодів двійкових чисел мав доповняльний код результату. Отже, віднімання чисел довільного знака можна звести до операції додавання:

.
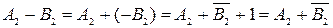