Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Перетворення числової інформації

У процесі перетворення інформації, яку несуть цифрові сигнали, у цифровій системі (пристрої) виникає необхідність переводу чисел з однієї системи числення в іншу еквівалентну систему. Це означає що, наприклад, десятковому числу має відповідати двійкове число :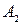

(1.2)

де =0, 1, 2,..., 9 – цифра в і-му розряді ()-розрядного числа (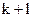)-розр’ядного двійкового числа 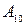; 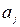=0 або 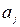=1 – цифра в j-му розряді (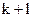)-розрядного двійкового числа .

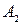Перевід чисел з будь-якої позиційної системи числення у код “10”. Для цього досить скористатися виразом (1.1), з допомогою якого розрахована сума ряду дає шуканий результат.

Розглдаємо тепер перевід чисел у різних системах числення. Загальним правилом переводу числа з однієї системи числення до іншої є виконання таких послідовних кроків:

1. Ділення в цілих числах заданого числа 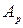на основу p-тої системи, в яку переводиться дане число ;

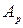2. Якщо частка не дорівнює нулю, її слід взяти за нове число повторити операцію п.1; якщо частка дорівнює нулю, перейти до п.З;

3. Виписати всі остачі у зворотному порядку, починаючи з останньої їх за цифри шуканого числа .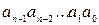

Двійкове число записується у вигляді цілих частин чисел, які отримані при перемноженні тільки дробової частини, починаючи зверху після коми. При цьому

задається точність результату. Отже, у даному випадку 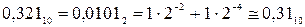. Таким чином, остаточно отримуємо рівність 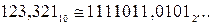Результат одержано з точністю 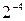. За такими самими правилами виконуються взаємні перетворення (переводи) в інших системах числення. Тільки при цьому ділити або множити потрібно на число, яке дорівнює основі тієї системи числення, до якої треба

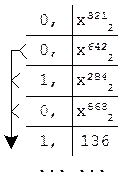
перейти.

На прикладі переводу з десяткової системи числення у двійкову покажемо більш спрощені форми запису обчислень. Наприклад, послідовне ділення числа 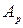на основу нової системи числення можна виконати у вигляді стовпчика, записуючи у лівому стовпчику (під числом 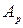) частку, а у правому – відповідну остачу. При переводі у двійкову систему це дуже просто виконати, бо для парних остач результат дорівнює нулю, для непарних – одиниці.

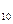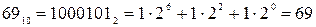Наприклад, переведемо число 69 у еквівалентне двійкове число: Іноді для переводу, з однієї системи числення до іншої розкладанням у ряд зручно скористатися такими рівностями: Проілюструємо цей спосіб спрощеного переводу на прикладах: ;

;

.
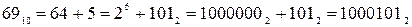
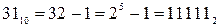
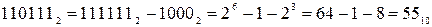