
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Матрица корреляций
|
|
| 0, 730 | 0, 710 | 0, 810 | 0, 560 | 0, 373 | 0, 319 | ||
| 0, 0730 | 0, 696 | 0, 650 | 0, 277 | 0, 047 | 0, 649 | ||
| 0, 710 | 0, 696 | 0, 538 | 0, 311 | 0, 049 | 0, 356 | ||
| 0, 810 | 0, 650 | 0, 538 | 0, 690 | 0, 560 | 0, 383 | ||
| 0, 560 | 0, 277 | 0, 311 | 0, 690 | 0, 680 | -0, 063 | ||
| 0, 373 | 0, 047 | 0, 049 | 0, 560 | 0, 680 | -0, 030 | ||
| 0, 319 | 0, 469 | 0, 356 | 0, 383 | -0, 063 | -0, 030 |
Таблица 11
Матрица факторных весов
| Переменные | Факторы | |||
| I | II | III | 
| |
| 0, 886 | 0, 075 | -0, 233 | 0, 845 | |
| 0, 777 | 0, 511 | 0, 088 | 0, 873 | |
| 0, 693 | 0, 390 | -0, 361 | 0, 763 | |
| 0, 913 | -0, 189 | 0, 089 | 0, 877 | |
| 0, 646 | -0, 560 | -0, 185 | 0, 765 | |
| 0, 485 | -0, 635 | 0, 065 | 0, 643 | |
| 0, 465 | 0, 447 | 0, 447 | 0, 613 |
Таблица 12
Простая структура
| Переменные | Факторы | Переменные | Факторы | ||||
| I | II | III | I | II | III | ||
| 0, 482 | 0, 193 | -0, 094 | 0, 148 | 0, 617 | -0, 193 | ||
| 0, 319 | -0, 044 | 0, 282 | -0, 147 | 0, 727 | 0, 015 | ||
| 0, 653 | -0, 192 | -0, 189 | -0, 109 | 0, 047 | 0, 576 | ||
| 0, 109 | 0, 562 | 0, 170 |
Из матрицы простых структур следует, что выделено три фактора, которые суть:
I—экономический статус, объединяющий 1, 2, 3 переменные;
II— семейный статус, объединяющий 4, 5, 6 переменные;
III — национальный статус, обусловленный 7-й переменной.
Прайс рассмотрел 93 города США по 15 рубрикам для 1930г.[156]:
1) население;
2)процент занятости в необслуживающей сфере;
3) соотношение полов;
4) процент прироста населения с 1925 по 1930 г.
5) средний месячный доход;
6)процент незанятого населения;
7) возраст города;
8) процент населения в возрасте от 15 до 50 лет;
9) процент работающих лиц со стажем в 10 лет и выше;
10) процент семенных рабочих;
11) средний объем семьи;
12) оптовая торговля на душу населения;
13) розничная торговля на душу населения;
14) относительный рост заработка;
15) процент налогоплательщиков.
Таким образом, дана эмпирическая матрица. По строкам расположены значения данных 15 переменных для каждого из 93 городов, по столбцам — значения каждой переменной для всех 93 городов. Матрица имеет 93 строки и 15 столбцов. Были получены коэффициенты корреляций для данных 15 переменных и благодаря матрице корреляций (15x15) найдены четыре фактора. Первый фактор наиболее сильно коррелирует с переменными 7, 1, 15, т.е. возрастом города, объемом населения, числом налогоплательщиков, торговлей на душу населения. Он может рассматриваться как экономический фактор (табл. 13).
Далее выводятся индексы городов по каждому фактору по формуле  =
=  z
z 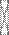

где f 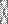 — индекс для фактора j, a
— индекс для фактора j, a 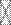 — факторный вес i -й переменной по j -му фактору, z
— факторный вес i -й переменной по j -му фактору, z 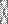 — стандартный балл i -й переменной. Для каждого фактора города ранжируются по величине его индекса.
— стандартный балл i -й переменной. Для каждого фактора города ранжируются по величине его индекса.
Таблица 13
Таблица факторных весов для 15-ти переменных
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
| Переменные | Факторы | |||
| I | II | Ш | IV | |
| 0, 6401 | 0, 0767 | 0, 2927 | -0, 1172 | |
| -0, 0439 | -0, 7251 | -0, 0181 | -0, 0888 | |
| -0, 0792 | -0, 3338 | 0, 7905 | 0, 1609 | |
| -0, 3761 | 0, 3891 | 0, 3023 | 0, 0259 | |
| 0, 5124 | 0, 2212 | 0, 6022 | 0, 0090 | |
| 0, 1178 | -0, 3537 | 0, 0620 | -0, 0343 | |
| 0, 7734 | 0, 0698 | 0, 0357 | -0, 0707 | |
| 0, 0057 | 0, 6399 | 0, 4464 | 0, 0652 | |
| 0, 2233 | 0, 6283 | -0, 0588 | 0, 0306 | |
| 0, 2546 | 0, 5121 | -0, 7299 | -0, 1637 | |
| 0, 0732 | -0, 6473 | -0, 2331 | -0, 1915 | |
| 0, 3123 | 0, 2410 | -0, 0801 | 0, 7991 | |
| 0, 3345 | 0, 2564 | 0, 1236 | 0, 8367 | |
| 0, 2063 | -0, 2817 | 0, 7849 | 0, 0986 | |
| 0, 5008 | 0, 1332 | 0, 3609 | 0, 0908 |
Мозер исследовал 157 городов по 57 характеристикам и получил такие четыре фактора: классовость, изменение населения за 1931—1951 гг., изменение населения за 1951—1958 гг. и перенаселенность города[157].
Из советских социологов Т. И. Заславская применила факторный анализ в исследовании причин миграции сельского населения[158]. По результатам анализа она пришла к выводу,
Таблица 14
Распределение признаков по факторам (в зависимости от максимальных весов)
| № фактора | № признака | Признак, имеющий максимальный вес по данному фактору | Коэффициент связи между показателем и фактором |
| I | Число врачей на 1000 сельских жителей | 0, 90 | |
| Оборот розничной торговли на сельского жителя | -0, 89 | ||
| Средняя оплата рабочего дня в совхозах | 0, 88 | ||
| Число кинопосещений на одного жителя в год | 0, 84 | ||
| Число медработников на 1000 сельских жителей | 0, 82 | ||
| Изменение численности рабочей силы совхозов | 0, 74 | ||
| Потребление электроэнергии в быту | 0, 67 | ||
| Обеспеченность жильем за счет совхозов | 0, 66 | ||
| Доля молодежи среди сельского населения | 0, 66 | ||
| Число учителей на 1000 сельских жителей | 0, 58 | ||
| Процент детей в детских учреждениях | 0, 34 | ||
| II | Естественный прирост населения, % | 0, 68 | |
| Доля лиц со средним и высшим образованием | 0, 60 | ||
| Плотность сельского населения | 0, 60 | ||
| Плотность железных и шоссейных дорог | 0, 57 | ||
| Доля лиц коренной национальности | 0, 54 | ||
| III | Процент домов без электричества | 0, 67 | |
| Число рабочих дней в году на работника | 0, 66 | ||
| Доля женщин среди работников совхозов | 0, 61 | ||
| Процент сельского населения в районе | 0, 52 | ||
| IV | Средний размер населенного пункта | 0, 67 | |
| Средний доход от личного подсобного хозяйства | 0, 43 |
что в миграции играют роль два главных фактора. Первый связан с материальным и культурным благосостоянием сельского населения района. Второй — с уровнем жилищно-бытового строительства.
Другим примером применения факторного анализа может служить анализ структуры признакового пространства, описывающего условия труда и жизни сельского населения различных районов[159]. Для испытания было отобрано 22 показателя. Весь анализ можно разделить на четыре стадии. Первая стадия — получение так называемой матрицы интеркорреляций.
Вторая стадия — это последовательное преобразование исходной матрицы и выполнение расчетов, направленных на «извлечение» независимых факторов, характеризующих внутреннюю структуру изучаемого признакового пространства.
Третья стадия представляет собою специальную операцию — поворот осей, которая результируется в составлении окончательной таблицы данных связи между признаками и факторами. Рассматривая, как улучшились качественные характеристики матрицы в результате поворота осей, авторы Т. И. Заславская и Е. В. Виноградова делают следующее заключение: «Несмотря на то, что использованные методы поворота осей носили приближенный характер и не обеспечивали оптимального результата, эффективность этой операции очевидна. Количество нежелательных средних весов уменьшилось почти вдвое, заметно повысилось число показателей, имеющих четко выраженные максимумы по отдельным факторам при малых значениях весов по другим. Показатели более равномерно распределились по факторам, что облегчило возможность предметного толкования последних»[160].
Последняя стадия факторного анализа заключается в трактовке результатов. Анализируя данные о распределении признаков по факторам в зависимости от максимальных весов, сведенные в специальную таблицу, авторы дают специфическое толкование каждому из четырех выделенных факторов. Тем самым каждый из выделяемых факторов получает содержательную характеристику через систему отношений к заданным внешним признакам. Первый фактор, объединяющий признаки 29, 49, 2, 42, 31, 1, 13, 12, 25, 47, 41, характеризуется авторами как уровень материально-бытовых и социально-культурных условий жизни сельского населения; второй, объединяющий признаки 57, 26, 7, 11, 10, — как структура сельского населения районов; третий, объединяющий признаки 15, 3, 53, 14, — как уровень экономического и технического развития района; и, наконец, четвертый, объединяющий признаки 6 и 4, — как характер сельского расселения (табл. 14).
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Во всех рассмотренных случаях использовались корреляции между переменными. Математически совершенно равноправна операция использования корреляций между лицами, т.е. между строками в эмпирической матрице. Это так называемая Q-техника, в отличие от наиболее употребительной R-техники. Q-техника приводит к нахождению факторов среди лиц (объектов), т.е. лица объединяются в группы-факторы. Эта техника весьма перспективна в социологии, хотя она и сопряжена с более трудоемкими операциями в сравнении с R-техникой[161].
Применение факторного анализа связано с математическими трудностями и с вопросом содержательной интерпретации факторов. Преодолеть эти трудности можно только широким экспериментированием по трем направлениям, применяя различные методы факторизации к разным выборкам, разным лицам и разным проблемам, что в целом и делается в большей части современных социологических исследований. По словам известного математика и психолога П. Хорста, “многие другие возможности применения факторного анализа, без сомнения, будут обнаружены в будущем, потому что роль факторного анализа значительна в систематическом научном исследовании во всех областях; его использование будет расширяться, его техника улучшаться, методы анализа – становиться более общими и доступными благодаря вычислительным машинам с большими скоростями работы”[162].
Основные понятия латентного анализа
Латентный анализ был развит П. Лазарсфельдом во второй половине 40-х годов ХХ в. в процессе изучения социальных установок американских солдат. Метод впервые был изложен в четвертом томе серии “Исследования по социальной психологии во второй мировой войне[163].
Существо метода заключается в следующем. Предполагается, как и в теории тестов, что исследуемая социальная установка представляет собой в числовом отношении некоторый гипотетический (латентный) континуум. Индивиды будут как-то располагаться на этом континууме в соответствии с определенным значением своей социальной установки. Индивидам задаются
вопросы, и ответы на вопросы выражают как бы внешнюю эмпирическую структуру исследуемого социального явления.
Задача метода – в установлении внутренней латентной структуры, которая обусловливает именно данный характер ответов. Первоначально для простоты будем считать вопросы дихотомическими, т.е. ответы на них альтернативны, типа “да – нет”. Вообще говоря, метод не связан с этим ограничением. На исследуемом континууме мы не можем ввести единицу измерения и начало отсчета. Поэтому в лучшем случае мы будем получать ординальную шкалу измерения. При исследовании данной социальной установки можно давать различные наборы вопросов. Вполне понятно, что вовсе необязательно при каждой эмпирической структуре (она, естественно, будет различна) индивид будет обладать одной и той же латентной структурой, т.е. быть в той же самой точке континуума. Не существует детерминистского проецирования эмпирической структуры (ответов) на латентную структуру, а можно попытаться определить только вероятность, с какой данная структура ответов соответствует определенной точке латентного континуума.
Вводится так называемая функция i -го вопроса  . Это вероятность положительного ответа индивида на i -й вопрос, при условии, если индивид находится в точке x латентного континуума. Функция вопроса (в английской транскрипции – traceline) введена Лазарсфельдом по аналогии с операционной характеристикой теории тестов и является вероятностной характеристикой вопроса. Можно выделить три типа вопроса по виду их функций (рис. 16).
. Это вероятность положительного ответа индивида на i -й вопрос, при условии, если индивид находится в точке x латентного континуума. Функция вопроса (в английской транскрипции – traceline) введена Лазарсфельдом по аналогии с операционной характеристикой теории тестов и является вероятностной характеристикой вопроса. Можно выделить три типа вопроса по виду их функций (рис. 16).
Тип 1 – это такие вопросы, когда с увеличением значений латентной переменной вероятность ответить на него положительно увеличивается, с уменьшением – уменьшается. Пока мы не обращаем внимания на форму кривой.
Тип II – зависимость обратная: с увеличением исследуемой переменной вероятность положительного ответа уменьшается.
Тип III – вопросы таковы, что наибольшая вероятность ответить на них положительно при среднем значении переменной; вероятность уменьшается при увеличении и уменьшении исследуемой переменной.
Далее вводится так называемый маргинал i -го вопроса – 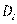 . Это число лиц, которые положительно ответили на i -й вопрос.
. Это число лиц, которые положительно ответили на i -й вопрос.
Наконец, поскольку задача вероятностная, необходимо найти закон распределения лиц на континууме, т.е. плотность вероятности  .
.
Таким образом, нам даны и вопросов (дихотомических), введены величины:
 – функции вопросов;
– функции вопросов;
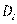 – маргиналы вопросов;
– маргиналы вопросов;
 – закон распределения лиц на латентном континууме;
– закон распределения лиц на латентном континууме;
 – число лиц в интервале х и x+dx;
– число лиц в интервале х и x+dx;
 – число лиц в интервале х и x+dx, которые положительно ответили на i -й вопрос;
– число лиц в интервале х и x+dx, которые положительно ответили на i -й вопрос;
 – число лиц на всем континууме, которые положительно ответили на i -й вопрос, т.е. это число равно маргиналу
– число лиц на всем континууме, которые положительно ответили на i -й вопрос, т.е. это число равно маргиналу 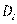 –известной величине.
–известной величине.
Отсюда основное расчетное уравнение латентного анализа:

Слева – эмпирические переменные (которые мы получаем в опыте), справа – латентные переменные, которые нам неизвестны. Цель исследования – нахождение функции  .
.

Вводится основное математическое допущение, “условие локальной независимости”. Оно заключается в том, что если взяты два вопроса, то для индивида в точке Х вероятность положительно ответить одновременно на оба вопроса, которую обозначим  , равна произведению вероятностей положительного ответа на каждый вопрос:
, равна произведению вероятностей положительного ответа на каждый вопрос:
 (2)
(2)
В общем виде, если взято k вопросов, уравнение (2) принимает вид
 (3)
(3)
В случае уравнения (1) мы для n вопросов получим следующую систему уравнений:
 , (4)
, (4)
где  – все наборы индексов i, j...
– все наборы индексов i, j...
Общего решения эта система уравнений не имеет. В зависимости от условий, налагаемых на функции, получаются те или иные модификации основного расчетного уравнения, которые называются моделями латентного анализа.
Некоторые модели допускают решение и в настоящее время все интенсивнее проникают в практику социологического измерения.
Рассмотрим различные варианты соотношения эмпирических и латентных переменных. Существуют следующие важные комбинации:
Тип I – это наиболее общая и сильная модель латентного анализа. Она может получиться в том случае, если на входе будут стоять качественные эмпирические переменные, а на выходе –количественные латентные переменные, т.е. из данных, обладающих весьма малой информацией, мы получаем весьма богатую информацию. Грубо говоря, мы задаем дихотомические вопросы (номинальная шкала измерения) респондентам в отношении удовлетворенности жизнью, а получаем по меньшей мере интервальную шкалу удовлетворенности.
Тип II – качественные эмпирические и качественные латентные переменные; наиболее разработанный тип моделей – модели так называемых латентных классов, когда все респонденты расположены не непрерывно на латентном континууме, а в отдельных точках, классах. Эти модели наиболее разработаны, во-первых, для дихотомических вопросов, во-вторых, для ограниченного числа вопросов и классов. Под классами понимается простая классификация или номинальная шкала измерения. Делаются в настоящее время попытки получить модель упорядоченных классов.
Тип III – количественные эмпирические и количественные латентные переменные. Эта модель латентного анализа имеет определенный аналог с факторным анализом.
Тип IV – количественные эмпирические и качественные латентные переменные. Это так называемая модель латентно-профильного анализа, разработанного Гибсоном.
Лазарсфельд предложил обобщить латентный анализ на случай многомерного латентного континуума. Для большей наглядности
приведем следующий пример. Когда мы исследуем удовлетворенность жизнью, то задаем определенные вопросы и пытаемся решить соответствующее расчетное уравнение латентного анализа, считая, что удовлетворенность жизнью представляет собой некоторую одномерную величину. Это понятие можно уточнить, если считать, что она – результат, к примеру, удовлетворенности работой и удовлетворенности личной жизнью. Тогда наша первоначальная латентная переменная заменяется двумя тоже латентными переменными, которые мы и будем искать.
В этом случае мы имеем не одномерный континуум – линию, на которой мы строили функции вопросов и функции распределения лиц, а двумерный континуум – плоскость. На ней будут уже поверхности – двумерные функции вопросов и двумерные функции распределения лиц.
Если обозначить одну латентную переменную х, а другую – у,
то основное расчетное уравнение (4) для двумерного случая перейдет в
 (5)
(5)
где  –набор индексов i, j...
–набор индексов i, j...
В последнее время делаются попытки применить латентный анализ к исследованию процессов. В частности, предложена модель применения метода латентных классов к простейшему марковскому процессу повторного поведения.
Существо модели латентных классов заключается в том, что латентная переменная считается прерывной[164]. Это означает, что все респонденты расположены в дискретных точках – классах. Будем считать, что задано n дихотомических вопросов, а респонденты расположены в m латентных классах. Для этого случая преобразуем основное уравнение (4).
Вместо непрерывной функции плотности будем иметь т частот, которые соответствуют относительным объемам латентных классов.
Обозначим их  ,
,  =1, 2,..., т. Вместо непрерывного графика i -го вопроса получатся отдельные вероятности для каждого класса, которые обозначим
=1, 2,..., т. Вместо непрерывного графика i -го вопроса получатся отдельные вероятности для каждого класса, которые обозначим  . Это вероятность положительного ответа на i -й вопрос в классе
. Это вероятность положительного ответа на i -й вопрос в классе  . Условие локальной независимости (3) будет иметь вид
. Условие локальной независимости (3) будет иметь вид
 . (6)
. (6)
Основные уравнения примут вид

 =1,..., т. (7)
=1,..., т. (7)
где  – наборы индексов.
– наборы индексов.
Важная сторона модели латентных классов –число эмпирических данных и число латентных (неизвестных) переменных. Как известно, необходимым условием существования решения системы латентных уравнений является тот факт, что число неизвестных должно быть не больше числа уравнений. Число уравнений 2".
Имеем

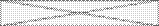 (7*)
(7*)
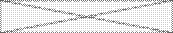
В 1-й строке – 1 уравнение ( );
);
во 2-й строке – n уравнений 
в 3-й строке –  уравнений
уравнений  .
.
.......................
В i -й строке – 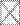 уравнений. Всего n строк, и, следовательно, общее число уравнений равно сумме биноминальных коэффициентов:
уравнений. Всего n строк, и, следовательно, общее число уравнений равно сумме биноминальных коэффициентов:
 .Число неизвестных латентных параметров равно m (n + 1), поскольку mn –число латентных вероятностей и т –число латентных частот в классах.
.Число неизвестных латентных параметров равно m (n + 1), поскольку mn –число латентных вероятностей и т –число латентных частот в классах.
Таким образом, необходимое (но недостаточное) условие разрешимости модели латентных классов соблюдено –
 . (8)
. (8)
Если окажется, что  , то необходимы такие дополнительные условия, налагаемые на эмпирические переменные, чтобы
, то необходимы такие дополнительные условия, налагаемые на эмпирические переменные, чтобы
 (9)
(9)
Только в этом случае модель имеет решение. Условия, налагаемые на эмпирические данные, называются условиями редуцируемости.
Из нескольких других оснований, связанных с решением расчетных уравнений, можно получить, что
 (8')
(8')
Объединяя условия (8) и (8'), получаем выражение, которое дает значение наименьшего числа вопросов:
 (8")
(8")
Очевидно, что модель латентных классов может иметь практическое значе
 |
ние только при небольшом числе вопросов. Дело здесь даже не в том, что это приведет к огромной вычислительной работе. Можно легко увидеть, уравнение (9) выполняется для
 и
и  . Проведем вычисления по всем этапам латентного анализа для этого случая.
. Проведем вычисления по всем этапам латентного анализа для этого случая.
Основные уравнения (7) примут вид
Или в развернутом виде:




| 


|
и мы имеем уравнение частот:

Всего восемь уравнений и восемь неизвестных; тем самым можно найти все восемь неизвестных параметров:


Весьма важной задачей латентного анализа является вычисление условных вероятностей. Последняя означает вероятность того, что индивид с данным вариантом ответа попадает в i -й класс:


из обшей формулы Бейесса

Лица тех вариантов ответов, у которых  попадают в один класс, а у которых
попадают в один класс, а у которых  – в другой класс (в случае двух классов). Эта ситуация сходна с операцией отнесения к факторам в факторном анализе.
– в другой класс (в случае двух классов). Эта ситуация сходна с операцией отнесения к факторам в факторном анализе.
Для решения уравнений модели латентных классов Лазарсфельд развил специальную алгебру, так называемую алгебру дихотомических систем. Основная идея решения вытекает из рассмотрения четырехклеточной таблицы.
| + | i -й – | вопрос | |
| j -й вопрос + | 
| 
| 
|
| – | 
| 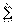
| 
|

| 
|
где  – относительное число лиц, которые положительно ответили на i -й и j-й вопросы;
– относительное число лиц, которые положительно ответили на i -й и j-й вопросы;  –число лиц, которые положительно ответили на j-й вопрос и отрицательно – на i -й;
–число лиц, которые положительно ответили на j-й вопрос и отрицательно – на i -й;  – число лиц, которые положительно ответили на i -й вопрос и отрицательно – на j-й;
– число лиц, которые положительно ответили на i -й вопрос и отрицательно – на j-й; 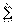 – число лиц, отрицательно ответивших на оба вопроса.
– число лиц, отрицательно ответивших на оба вопроса.
Рассмотрим определитель

Поскольку из таблицы



то имеем




Назовем определитель [ ij ]произведением двух вопросов – i -го и j -го. На этом определителе основываются три меры связи между
l47
дихотомическими вопросами четырехпольной таблицы:

 ;
;  .
.
Для трех вопросов – i, j, k – введем понятие условного произведения  .
.
Выразим неизвестные параметры системы через определители, значения которых известны на основе эмпирических данных. Имеем
 .
.
Представим последний определитель как произведение таких определителей:
 .
.
Следует отметить, что, по крайней мере, один определитель [ ij ](ij = 1, 2, 3) не равен нулю; в противном случае все три вопроса независимы и не имеют никакого отношения к исследуемому явлению.
Введем обозначение:
 i = 1, 2, 3.
i = 1, 2, 3.
Соберем вместе все имеющиеся уравнения для нашего случая трех вопросов и двух латентных классов:
 (I)
(I)
 (II)
(II)
 (III)
(III)
 . (IV)
. (IV)
Рассмотрим величину

или
 .
.
Но из (IV)  .
.
Отсюда
 .
.
Следовательно,  и
и  являются корнями некоторого квадратного уравнения
являются корнями некоторого квадратного уравнения
 . (11)
. (11)
Мы положили, что 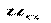 и ищем параметры для третьего вопроса (в случае, если
и ищем параметры для третьего вопроса (в случае, если  , то мы будем искать параметры такого вопроса, где определитель других двух не равен нулю).
, то мы будем искать параметры такого вопроса, где определитель других двух не равен нулю).
Как только  и
и  найдены, все остальные параметры можно найти без труда.
найдены, все остальные параметры можно найти без труда.
Имеем, по определению,

 (12)
(12)
Получаем  и
и  .
.
Далее имеем две системы линейных уравнений:


 (13)
(13)
 (14)
(14)
из которых получаем  ,
,  ,
,  ,
,  .
.
Проводя вычисления уравнений (11) – (14), получаем значения маргиналов для классов, т.е.
 ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Зная эти величины, можно получить частоты вариантов ответов для классов. Например, если берем ответный вариант – + –, то его частота в классе 1 равна
 , где
, где 
 а для класса 2 соответственно равна
а для класса 2 соответственно равна
 , где
, где 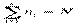
 .
.
Таким образом последовательно получаем все частоты вариантов ответов.
Основное расчетное уравнение допускает возможность решения при определенных ограничениях, наложенных не на  , а на функцию
, а на функцию  . Допустим, что функции вопросов выражаются
. Допустим, что функции вопросов выражаются
некоторыми полиномами

В общем случае – степенью k. Для простоты рассмотрим только случаи k =1 и k =2, т.е. когда функции вопросов – прямые и параболы. Прежде всего возьмем случай k = l:

из(1)

 .
.
Интегралы суть моменты функции  :
:
 .
.
Далее, условия локальной независимости:
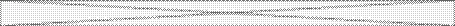
 .
.
Можно заметить, что для двух вопросов будет шесть неизвестных 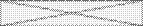 и три уравнения; для трех вопросов – восемь неизвестных и семь уравнений; для четырех вопросов – десять неизвестных и 16 уравнений.
и три уравнения; для трех вопросов – восемь неизвестных и семь уравнений; для четырех вопросов – десять неизвестных и 16 уравнений.
Аналогичные выкладки можно произвести для случая квадратной функции вопросов:


l50

 .
.
Имеем  .
.
Оказывается, что
 , где
, где  .
.
Аналогично


Введем величину
 .
.
Тогда можно выразить коэффициенты линейной функции вопроса  на основании эмпирических данных
на основании эмпирических данных  и
и  :
:

 .
.
Два первых момента – средняя и дисперсия – не определяются. Полагаем их равными соответственно нулю и единице. В таком случае можно легко определить третий момент функции  :
:
 ,
,
где
 .
.
Зная функции вопросов, можно получить все последующие моменты  .Например, с помощью
.Например, с помощью  имеем выражение
имеем выражение
изкоторого легко определяется  . Добавляя уравнения для других совместных частот, получим моменты высших порядков, и таким образом
. Добавляя уравнения для других совместных частот, получим моменты высших порядков, и таким образом  будет определена.
будет определена.
|
|
