
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Постановка проблемы измерения в многомерной статистике
|
|
С развитием многомерной статистики многие ее методы начали в целях измерения с успехом использоваться в социальных исследованиях: социологии, демографии, психологии. Исторически первым таким методом является факторный анализ. Первоначально он был развит в применении к количественным данным, получаемым в психологическом тестировании. Спустя несколько десятилетий, в 40-х годах был развит так называемый латентный анализ в применении к качественным данным социологии и социальной психологии. В последнее время для реализации вероятностной классификации в социологии начала использоваться методика распознавания образов.
Современный аппарат многомерной статистики позволяет выработать единый подход к проблеме измерения данных любой природы — количественных и качественных. Предположим, мы хотим измерить отношение к труду посредством анкеты. Ответы на вопросы будут представлять собой некоторые значения эмпирической переменной. Изучаемое отношение к труду можно рассматривать как некоторую гипотетическую (латентную) переменную, причем, и это существенно, как в данном случае, одномерную переменную. Если анкета имеет n вопросов, то эмпирическая переменная будет n -мерной величиной (n -мерным вектором), а исследуемая латентная переменная — одномерным вектором. В общем случае латентная переменная может быть представлена m -мерным вектором. Большая трудность связана с характером компонент эмпирического и латентного векторов. В шкалах Лайкерта и Терстона латентная переменная представлялась порядковой переменной, а эмпирические переменные n -мерным
вектором (по числу вопросов в вопроснике), причем каждая компонента векторов была количественной переменной. В принципе компоненты обоих векторов могут быть величинами любой природы.
В общем случае обозначим эмпирическую переменную, состоящую из n компонентов, х, aлатентную переменную, состоящую из т компонентов, — у. Когда индивид отвечает на вопросы анкеты, то это означает, что он, обладая определенным значением латентной переменной у, реализует определенное значение эмпирической переменной, т.е. можно предположить, что существует условное распределение х и у [150]:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
F(x|y).
Нам неизвестно распределение латентной переменной у — L(y), но из данных ответов мы получаем безусловное распределение х — Н(х). Эти три функции распределения — F(х|у), L(y), H(x) — связаны известным соотношением:
H(x)= 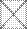 (x|y)dL(y).
(x|y)dL(y).
Если бы нам были известны функции F и L, то проблема оценки латентной переменной у из наблюдаемой (эмпирической) переменной х сводилась бы к проблеме Бейеса. Однако обычно F и L неизвестны. В общем виде предложенное интегральное уравнение не решается. Для того чтобы получить его решение н, следовательно, решить проблему измерения латентной переменной у через посредство эмпирической переменной х, необходимо наложить на F и L определенные ограничения. Т. Андерсон вводит два ограничения: предположение об условной независимости и предположение о линейной регрессии. Предположение об условной независимости можно записать таким образом:
F(x|y)=  ,
,
и оно означает, что эмпирические переменные  распределены независимо при данном значении латентной переменной у. В переводе на простой язык это говорит о том, что определенный ответ на какой-то вопрос анкеты не влияет на ответы на другие вопросы, предполагая, что индивид в момент ответа обладает присущим ему, но неизвестным значением исследуемой латент-
распределены независимо при данном значении латентной переменной у. В переводе на простой язык это говорит о том, что определенный ответ на какой-то вопрос анкеты не влияет на ответы на другие вопросы, предполагая, что индивид в момент ответа обладает присущим ему, но неизвестным значением исследуемой латент-
ной переменной. Это предположение используем при определении моментов распределения F(x|y).
По определению, первый момент:
Е(х|у)=  (у).
(у).
Второй момент:
 .
.
В силу предположения условной независимости матрица D(y) диагональная ( =0, i
=0, i  j) и выражение для второго момента принимает вид:
j) и выражение для второго момента принимает вид:
 .
.
Второе предположение о линейности регрессии записывается в виде
 ,
,
что означает, что среднее х при данном у представляет собой линейную функцию от у, где  — матрица размерности пт.
— матрица размерности пт.
Без потери общности можно принять, что
Еу=0, Еуу'=М.
Тогда
 .
.
Если положить М=J, то
 .
.
Таким образом, получаем модель факторного анализа: из известной ковариационной матрицы  определяем матрицу факторных нагрузок
определяем матрицу факторных нагрузок  (при выполнении второго предположения о линейности регрессии).
(при выполнении второго предположения о линейности регрессии).
Можно показать, что если х считать дихотомической переменной и функция F(x|y) определяет вероятность положительного ответа на х при данном у, то получается модель латентно-структурного анализа. В этом случае обозначим
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе

и функцию F(x|y) заменим на  (xi...
(xi...  у).
у).
Теперь наша задача — рассмотреть более детально использование моделей факторного и латентного анализа в социологии. Также мы остановимся на специальном варианте регрессионного анализа, который получил в литературе название причинного анализа.
Основные понятия факторного анализа
Факторный анализ был развит психологами в течение первой половины XX в., главным образом в работах Спирмена, Терстона, Кетелла и Хотелинга.
Начиная с 50-х годов он начал широко применяться в социологии, социальной психологии и во многих областях социального исследования. В последние годы — и это весьма характерно — он привлек внимание крупных специалистов математической статистики— Кенделла, Бартлета, Лоули — и представляет в настоящее время весьма разработанную математическую теорию.
Как и в случае шкалирования, мы имеем N лиц и n вопросов— переменных, т.е. таблицу (матрицу), в которой по строке расположены ответы лица на вопросы, а по столбцу — ответы лиц на определенный вопрос. Существенно, что переменные количественные, т.е. ответ выражается числом, выражающим реальное количественное отношение — возраст, доход, разряд и т.п. Смысл факторного анализа заключается в том, что принято считать данные п переменных линейными функциями меньшего числа других переменных, называемых факторами. Факторы выступают как бы более фундаментальными переменными, характеризующими явление, и исходные переменные как бы объединяются в группы, каждая из которых представляет некий фактор. Задача анализа — найти эти факторы.
Поскольку фактор представляет собой объединение определенных переменных, постольку из этого следует, что эти переменные связаны друг с другом, обладают корреляцией, причем большей между собой, чем с другими переменными, входящими в другой фактор. Методы отыскания факторов основываются на использовании именно коэффициентов корреляции между переменными. Факторный анализ дает нетривиальное решение, т.е. это решение нельзя предвидеть и усмотреть, не применяя специальную технику извлечения факторов. Вместе с тем его решение имеет большое значение для характеристики социального явления, поскольку вначале оно характеризовалось п переменными, а в результате применения анализа оказалось, что оно характеризуется меньшим числом — q — других переменных-факторов.
Первоначально Спирмен выдвинул идею одного так называемого генерального, фактора (g-фактор). Это означало, что вся деятельность индивида обусловлена влиянием одного генерального фактора. Смысл факторного анализа, по Спирмену, состоит в том, что «все стороны интеллектуальной активности вообще имеют одну фундаментальную функцию... в то время как
оставшиеся или специфические элементы деятельности, по-видимому, в каждом случае отличны от нее во всем другом»[151]. Если мы задаем индивидам вопросы, то, по Спирмену, необходимо установить влияние, зависимость ответов от действия генерального фактора, т.е. требуется установление корреляции переменных с фактором: большая корреляция — большая связь данной переменной (действия) с фактором и т.д.
Позднее Терстон обобщил идею Спирмена и Хольцингера в своей модели многофакторного анализа, в которой существует конечное множество факторов, которые обуславливают значение данной системы эмпирических переменных. Терстон применил аппарат матричной алгебры и создал весьма разработанный формализм факторного анализа[152]. Терстон проделал также большую работу в области методологии факторного анализа. Он подразделил факторный анализ на факторный анализ описания и факторный анализ объяснения.
Факторный анализ определенной эмпирической системы данных будет только описательным анализом данной системы, находясь в зависимости от выбора переменных и популяции. Но если при изучении явления применять факторный анализ на разных системах переменных и на разных популяциях и если при этом будут получаться однотипные факторы, то эти факторы уже будут объясняющими. Описательный факторный анализ дает факторную картину единичного явления, объясняющий позволяет найти внутренние глубинные переменные, которые обусловливают эмпирическую картину. Терстон сформулировал ряд условий, которым должна отвечать факторная система: простота, инвариантность, единственность. Собственно, это те методологические требования, которые предъявляются любой научной теории.
Факторный анализ является разделом многомерной статистики, поскольку популяция индивидов исследуется по n переменным (измерениям), характеризующимся n эмпирическими распределениями. Можно установить зависимости между ними, вычисляя коэффициенты корреляции. Переменные и их распределения распадутся на группы по величине коэффициентов корреляции. Например, первая переменная тесно связана со второй и третьей, а вторая — с третьей; с остальными переменными у этих переменных связь слабая. Они образуют как бы одно целое, одну функциональную единицу —фактор. Если переменных n, то коэффициенты корреляций между переменными образуют
квадратную симметричную матрицу порядка п. Здесь предполагается обычный коэффициент парной корреляции. В этом случае можно рассуждать и по-другому. В этом случае переменная может быть представлена как сумма факторов, умноженных на некоторые коэффициенты, которые определяются из матрицы корреляций. Будем искать такую переменную (фактор), когда при исключении ее влияния, частные коэффициенты корреляции между данными переменными будут равны нулю: rij, f 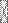 =0. Если же они не все оказались равными нулю, то ищем вторую переменную— фактор, чтобы при исключении действия этих двух факторов частные коэффициенты между данными переменными были бы равными нулю (rij, f
=0. Если же они не все оказались равными нулю, то ищем вторую переменную— фактор, чтобы при исключении действия этих двух факторов частные коэффициенты между данными переменными были бы равными нулю (rij, f 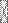 , f
, f  =0), и т.д.
=0), и т.д.
Процесс обрывается, например, на q факторе, если при учете этих q -факторов все частные коэффициенты между переменными будут равны нулю.
Теперь в несколько упрощенном виде выразим математически основную идею факторного анализа. Имеем N лиц и п переменных, т.е. эмпирические данные:  ; i= 1 ,..., n. Можно изобразить это в виде матрицы:
; i= 1 ,..., n. Можно изобразить это в виде матрицы:
X= 
Основная мысль факторного анализа[153] — представить эмпирические переменные в качестве линейных комбинаций меньшего числа некоторых других переменных, которые назовем факторами:
 . (1)
. (1)
Оказывается, что матрица эмпирических данных имеет связь с матрицей корреляций между эмпирическими переменными. Это видно из следующих преобразований.
Прежде всего нормируем  , т.е. положим, что
, т.е. положим, что
 ,
,
где  — средняя арифметическая j -й переменной;
— средняя арифметическая j -й переменной;  - стандартное отклонение j -й переменной.
- стандартное отклонение j -й переменной.
В этом случае
 ,
,  ,
,
т.е. средняя и дисперсия нормированных переменных соответственно равны нулю и единице.
Уравнение (1) можно переписать для нормированных данных:
 . (
. ( )
)
Впредь будем считать данные нормированными и использовать обозначения уравнения (1).
Уравнение (1) можно написать в матричной форме:
X=AF, (2)
где
A={ajk}=  ;
;
q< n, j= 1,..., n; k =1,..., q;
F={fki} = 
i = 1,..., N; k = 1,..., q.
По определению коэффициента линейной корреляции имеем (для нормированных данных)
 (3)
(3)
или в матричной форме
 , (4)
, (4)
где R — матрица корреляций:
R= 
X — матрица эмпирических данных; X' — транспонированная матрица X.
В уравнение (4) подставим уравнение (2):
R = 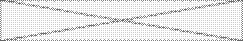 .
.
Выражение в скобках есть матрица корреляций между факторами. Будем считать, что факторы не коррелируют между собой или что они ортогональны. Тогда
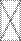 FF' = I,
FF' = I,
где I — единичная матрица.
В таком случае имеем
R=AA'. (5)
Уравнение (5) запишем в алгебраической форме:
 ; (6)
; (6)
 . (6
. (6 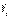 )
)
Уравнение (5) является основой для реализации процедуры факторного анализа. Слева мы имеем эмпирические данные — матрицу корреляций, справа — неизвестные величины, которыми являются элементы матрицы факторных нагрузок.
Вообще говоря, уравнение (1) весьма редко имеет место. Обычно переменная не точно обусловлена факторами, а обусловлена с ошибкой:
 ,
, 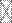 (7)
(7)
где  - величина ошибки.
- величина ошибки.
Как бы мы ни подбирали факторы, они точно не воспроизведут эмпирические переменные, а всегда — с некоторым приближением. Ошибка приближения или остаток обозначается вектором е. Уравнение (7) является основным уравнением факторного анализа.
В нем  — нормированы,
— нормированы,  — ортогональны и нормированы,
— ортогональны и нормированы,  — независимы, причем
— независимы, причем  = 0.
= 0.
Если бы мы имели дело с уравнением (1), то на главной диагонали матрицы корреляций стояли бы единицы. Но поскольку на практике приходится иметь дело с уравнением (7), то решение осложняется. Рассмотрим уравнение (6). Имеем rkk= 1.
Величина  представляет собой долю дисперсии факторов в общей дисперсии i -й переменной.
представляет собой долю дисперсии факторов в общей дисперсии i -й переменной.
Обозначим

и назовем ее факторной дисперсией, которая в общем виде нам неизвестна. Она и будет стоять на диагонали матрицы корреляций.
Теперь встает проблема, как решить уравнения (5) и (7), т.е., зная эмпирическую матрицу корреляций, нужно найти неизвестную матрицу факторных нагрузок. Это означает, что, зная  эмпирических коэффициентов корреляций, можно найти неизвестные величины a jk; j = l,..., n; k = l,..., q. Естественно, что числа п и q должны быть в определенной зависимости. Аналитически можно показать[154], что они должны удовлетворять неравенству
эмпирических коэффициентов корреляций, можно найти неизвестные величины a jk; j = l,..., n; k = l,..., q. Естественно, что числа п и q должны быть в определенной зависимости. Аналитически можно показать[154], что они должны удовлетворять неравенству
(n + q) < (n – q) 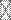 .
.
Методы решения основных уравнений факторного анализа называются методами факторизации. В настоящее время используются в основном два метода — центроидный и максимального правдоподобия. Остановимся на первом.
В матричной форме это выглядит так:
Х=АF+Е; (8)
ХХ'=АА'+ЕЕ'; (9)
 ; (10)
; (10)
 , i
, i  j. (11)
j. (11)
Перед тем как перейти к решению уравнения (5) факторного анализа, определим значение элементов входящих в него матриц.
Имеем уравнение (1):
 .
.
Множим его на  , суммируем по всем i и делим на N:
, суммируем по всем i и делим на N:
 ,
,
поскольку, как мы полагаем, факторы не коррелируют между собой и нормированы. Отсюда

по определению коэффициента корреляции.
Аналогичную процедуру можно проделать для каждой переменной, и потому получаем равенство  .
.
Факторная нагрузка  представляет собой коэффициент корреляции j -и переменной и
представляет собой коэффициент корреляции j -и переменной и  -го фактора.
-го фактора.
Существо центроидного метода заключается в следующем. Рассмотрим q -мерное пространство факторов и в нем n -векторов (переменных). Можно выбрать систему векторов
 ,
,
..........
 ,
,
где  — факторные нагрузки, i= 1 ,..., n; j =l,..., q.
— факторные нагрузки, i= 1 ,..., n; j =l,..., q.
Ищем координаты центроида (центра тяжести) векторов. Каждая из q -координат центроида равна среднеарифметическому соответствующих координат, а именно:
 , j = 1,..., q.
, j = 1,..., q.
Полагаем, что центроид лежит на оси координат. Тогда
 .
.
Его координаты суть
 ; 0; …; 0.
; 0; …; 0.
Найдем a 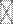 , k= 1,...., n; имеем
, k= 1,...., n; имеем
 .
.
Суммируем:
 ,
,
или
 .
.
Еще раз суммируем:
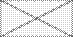
 .
.
Обозначим:
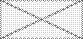 — сумма элементов k- гостолбца матрицы корреляций,
— сумма элементов k- гостолбца матрицы корреляций,
 — сумма всех элементов матрицы корреляций.
— сумма всех элементов матрицы корреляций.
Имеем
 , или
, или  .
.
Окончательно получаем 
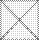 и находим все факторные нагрузки
и находим все факторные нагрузки  , первого фактора.
, первого фактора.
После этого находим остаточную матрицу корреляций:
 ;
;
 .
.
Или в матричной форме:
 = R – a
= R – a  ,
, 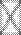
где W 1— остаточная матрица корреляций,  — вектор-строка матрицы факторных весов.
— вектор-строка матрицы факторных весов.
С остаточной матрицей W 1производим аналогичную процедуру, что и при извлечении первого фактора, с той только разницей, что отрицательные знаки у корреляций изменяем на положительные с тем, чтобы сделать дисперсию максимальной:
W2=R—  — ага'г.
— ага'г.
Затем аналогично находим W 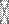 и т.д.
и т.д.
Количество шагов в нахождении остаточных матриц определяется числом факторов. В первоначальной матрице корреляций взяты приближенные значения факторных дисперсий. Как только при их значении определены факторные нагрузки, можно начать итерационный процесс — улучшить факторные дисперсии с помощью найденных факторных нагрузок: снова найти факторные нагрузки и снова улучшить факторные дисперсии и т.д. Как правило, итерация происходит достаточно быстро.
Найдем корреляцию между отметками 220 школьников по шести школьным предметам — французскому языку, английскому языку, истории, арифметике, алгебре, геометрии. Получаем матрицы I, II, III, IV (табл. 6, 7, 8, 9).
Таблица 6
I. Матрица корреляций *
| Гальский язык | (0, 439) | 0, 439 | 0, 410 | 0, 288 | 0, 329 | 0, 248 |
| Английский язык | 0, 439 | (0, 439) | 0, 351 | 0, 354 | 0, 320 | 0, 329 |
| История | 0, 410 | 0, 351 | (0, 410) | 0, 164 | 0, 190 | 0, 181 |
| Арифметика | 0, 288 | 0, 354 | 0, 164 | (0, 595) | 0, 595 | 0, 470 |
| Алгебра | 0, 329 | 0, 320 | 0, 190 | 0, 595 | (0, 595) | 0, 464 |
| Геометрия | 0, 248 | 0, 329 | 0, 181 | 0, 470 | 0, 464 | (0, 470) |
| Суммы | 2, 153 | 2, 232 | 1, 706 | 2, 466 | 2, 493 | 2, 162 |
| Нагрузки фактора I | 0, 592 | 0, 614 | 0, 614 | 0, 678 | 0, 686 | 0, 595 |
| * Лоули Дж., Максвелл А. Факторный анализ как статистический метод, с. 42—46. |
Таблица7
|
|
