Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Однопродуктова статична детермінована модель без дефіциту з «розривами» цін.

У розглянутій задачі не враховуються питомі витрати на придбання товарів, тому що вони постійні і не впливають не рівень запасу. Однак часто ціна одиниці товару залежить від розміру закуповуваної партії. У таких випадках ціни міняються стрибкоподібно, наприклад, при наданні оптових знижок. При цьому в моделі керування запасами необхідно враховувати витрати на придбання товарних запасів.

Розглянемо однопродуктову статичну детерміновану модель без дефіциту, у якій ціна одиниці товару дорівнює ц₁ при n < q і дорівнює ц₂ при n ≥ q, причому ц₁ > ц₂ і q – розмір замовлення, при перевищенні якого надається знижка.

Сумарні витрати в одиницю часу при n < q з урахуванням (7.8) і (7.3) рівні:

Сумарні витрати в одиницю часу при n ≥ q з урахуванням (7.8) і (7.3) рівні:

Мінімум функцій S₁(n) і S_q(n), відповідно до формули Уилсона, досягається в точці n₀ (7.10). З аналізу графіків функцій S₁(n) і S_q(n) (мал. 7.3) випливає, що оптимальний обсяг замовлення n* залежить від того, в якому місці відносно трьох показаних на мал.7.3 зон знаходиться точка розриву ціни q. Розташування зон визначається шляхом визначення невідомого q₁ (при відомому з (7.10) n₀) з рівняння S₁(n₀) = S_q(q₁).

Тоді зони розподіляються в такий спосіб:

Зона 1: 0 ≤ q < n₀;

Зона 2: n₀ ≤ q < q₁;

Зона 3: q ≥ q₁.

У залежності від розташування крапки розриву ціни q, оптимальний розмір замовлення визначається в такий спосіб:

n* =		n0, якщо 0 ≤ q < n0 (зона 1)
q, якщо n0 ≤ q < q1 (зона 2)	(18)
n0, якщо q ≥ q1 (зона 3)
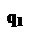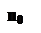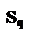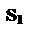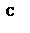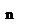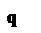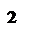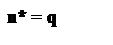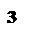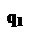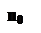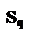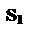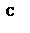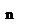
Мал. 7.3.

Алгоритм визначення n* можна подати в такому вигляді.

1. Визначити n₀. Якщо q < n₀ (зона 1), то рішення n* = n₀ отримане й алгоритм завершується. В іншому випадку переходимо до кроку 2.

2. Визначити q₁ з рівності S₁(n₀) = S_q(q₁) і установити, де відносно зон 2 і 3 знаходиться значення q:

а) якщо n₀ ≤ q < q₁ (зона 2), то n* = q;

б) якщо q ≥ q₁ (зона 3), то n* = n₀.