Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Однопродуктова статична детермінована модель без дефіциту.
|
|
Припущення про те, що дефіцит не допускається, означає повне задоволення попиту на продукт, що запасається, тобто функції b(t) і r(t) збігаються.
Розглянемо деякий інтервал часу θ (наприклад рік). Загальне споживання запасів за який складає N. У найпростішому випадку передбачається, що витрата запасу відбувається безупинно з постійною інтенсивністю, тобто b(t)= b. Ця інтенсивність визначається відношенням загального споживання продукту до часу, протягом якого він витрачається:
| b = | N | (7.3) |
| θ |
Поповнення запасу відбувається партіями однакового обсягу n через однакові відрізки часу Т. Оскільки інтенсивність витрати дорівнює b, то кожна партія буде використана за час Т
| Т = | n | (7.4) |
| b |
Таким чином функція a(t) не є безперервною:
| a(t) = |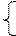 
| 0, t ≠ iT | |
| n, t = iT, i = 0, 1, … |
Іншими словами функція інтенсивності постачання a(t) є імпульсною, тобто запас поповнюється миттєво в моменти часу кратні T.
Якщо відлік часу почати з моменту надходження першої партії, то рівень запасу в початковий момент часу дорівнює обсягу цієї партії n, тобто J(0) = n.
На часовому інтервалі [0, T] рівень запасу зменшується по прямої J(t) = n - bt від значення n до 0. Оскільки дефіцит не допускається, то в момент часу T рівень запасу миттєво поповнюється до колишнього значення n за рахунок надходження партії запасу.
Процес зміни J(t) повторюється на кожному часовому інтервалі тривалістю T. Графічно залежність рівня запасу від часу ілюструється мал. 7.1.
          
|
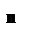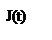
| Мал. 7.1. |
Таким чином, задача керування запасами полягає у визначенні такого обсягу партії n, при якому сумарні витрати на створення і збереження запасу були б мінімальними.
Позначимо через С сумарні витрати, витрати на створення запасу – через С1, витрати на збереження запасу – через С2, витрати на доставку однієї партії продукту, що не залежать від обсягу партії - с1, витрати на збереження однієї одиниці продукту в одиницю часу – с2. Оскільки за час θ необхідно запастися N одиницями продукту, що доставляється партіями обсягу n, то число таких партій k дорівнює:
| k = | N | = | θ | (7.5) |
| n | T |
Отже С1 = с1k = с1N/n (7.6)
Миттєві витрати на збереження запасу в момент часу t рівні с2 J(t). Тоді витрати на збереження за проміжок [0, T] складуть
Т T
с2 ∫ J(t) dt = с2 ∫ (n- bt) dt
0 0
або з урахуванням (7.4)
| Т с2 ∫ J(t) dt = 0 | с2 nТ | |||
Середній запас за проміжок [0, T] дорівнює nТ/2, тобто витрати на збереження всього запасу при лінійному часі його витрати дорівнюють витратам на збереження середнього запасу.
З урахуванням (7.5) одержуємо:
| с2 = | с2 nТ | k = | с2 n θ | (7.7) |
Відзначимо, що витрати С1 обернено пропорційні, а витрати С2 прямо пропорційні обсягу партії n.
З огляду на, що З = З1 + З2 сумарні витрати визначаються функцією витрат:
| С = | с1 N | + | с2 θ n | (7.8) |
| n |
Графіки залежностей С, С1, С2 зображені на мал. 7.2.
            
|
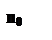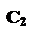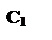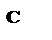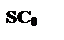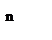
| Мал. 7.2. |
В точці минимума функції С(n) її похідна дорівнює 0:
| С’(n) = - | с1 N | + | с2 θ | = 0 | |
| n2 |
Тоді
| n = | n0 = |  
| 2с1 N | (7.9) |
| с2 θ |
або, з урахуванням (7.3)
| n0 = |
| 2с1b | (7.10) | |
| с2 |
Формула (7.10) називається формулою Уїлсона чи формулою найбільш економічного обсягу партії.
Зауважимо, що добуток С1С2 = 0, 5с1с2θ N є величина постійна. Як відомо сума двох співмножників приймає найменше значення, коли вони рівні між собою, тобто С1= С2 або
| с1 N | = | с2 n θ | (7.11) | ||
| n |
Рівність (7.11) легко перетворити до виду (7.9).
З (7.11) випливає, що мінімум загальних витрат задачі керування запасами досягається тоді, коли витрати на створення запасу дорівнюють витратам на збереження запасу. При цьому мінімальні сумарні витрати складають
| С0 = С(n0) = | 2с1 N | 
| (7.12) | |
| n |
звідки з урахуванням (7.5) и (7.9), отримуєм С0 = √ 2с1с2θ N або
| С0 = θ |
| 2с1 с1b | (7.13) |
Число оптимальних партій k0 за час θ з урахуванням (7.5), (7.9) і (7.3) дорівнює
| k0 = | N | = |
| с2 N θ | = θ |   
| с2 b | |
| n0 | 2с1 | 2с1 |
Час витрати оптимальної партії на підставі (7.4) з урахуванням (7.9) і (7.3) дорівнює
| T0 = | n0 | = n0 | θ | (7.14) | |
| b | N |
| T0 = |
| 2с1 θ | = |
| 2с1 | (7.15) | |
| с2 N | с2 b |
Приклад. Потреба складального підприємства в деталях деякого типу складає 120 000 деталей на рік, причому ці деталі витрачаються в процесі виробництва рівномірно і безупинно. Деталі замовляються раз на рік і постачаються партіями однакового обсягу, зазначеного в замовленні. Збереження деталі на складі коштує 0, 35 гр.о. на добу, а постачання партії – 10 000 гр.о. Простоювання виробництва через відсутність деталей неприпустимо.
Визначити найбільш економічний обсяг партії й інтервал між постачаннями, які потрібно вказати в замовленні (вважається, що постачальник не допускає затримок постачань).
Рішення. За умовою витрати на одну партію складають с1 = 10 000 гр.о., витрати на збереження одиниці запасу в добу с2 = 0, 35 гр.о. Загальний проміжок часу θ = 1 рік = 365 днів, а загальний обсяг запасу за цей період складає N = 120 000 деталей.
По формулі (7.9) визначається n0 ≈ 4335 деталей, а по формулі (7.14) T0 =13, 2 ≈ 13 днів.
Відповідь. Найбільш економічний обсяг партії n0 ≈ 4335 деталей.
Оптимальний інтервал часу між постачаннями T0 ≈ 13 днів.
|
|