💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Лекція 3. Транспортна задача.

Транспортна задача лінійного програмування відноситься до класу розподільних задач. Задачі цього типу виникають тоді, що коли наявних ресурсів недостатньо для виконання всіх операцій найбільш ефективним образом.

Метою рішення розподільних задач є відшукання такого розподілу ресурсів по операціях (споживачам), що або мінімізує загальні витрати на виконання операцій, або максимізує сумарний прибуток.

Транспортну задачу в загальному вигляді можна сформулювати так:

є n пунктів відправлення А₁, А₂, … А_m;

є m пунктів призначення 1, 2, … n.....

У пунктах відправлення є деяка кількість однорідного вантажу (потужність постачальника): Q₁, Q₂, … Q_m.....

Споживи пунктів призначення у вантажі (попит) складають q₁, q₂, … q_n.....

Витрати (коефіцієнт витрат) на перевезення від постачальника i до споживача j: с_ij.

Потрібно знайти обсяги перевезень х_ij з і в j, таким чином, щоб:

1) потужності всіх постачальників були реалізовані;

2) попит усіх споживачів був задоволений;

3) загальна вартість перевезення було мінімальною.

Цільова функція:

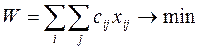(3.1)

Шуканий обсяг перевезення від і-го постачальника до j-му споживача х_ij назвемо постачанням клітки (i, j). Задані потужності постачальників і попити споживачів накладають обмеження на значення невідомих х_ij.

Для того, щоб потужність шкірного з постачальників була реалізована, необхідно скласти рівняння балансу (обмежень) для шкірного рядка таблиці постачань, тобто

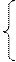
	х11 + х12 + … + х1n = Q1
	(3.2)
хm1 + хm2 + … + хmn = Qm

Аналогічно, щоб попит кожного зі споживачів був задоволений, подібні рівняння балансу (обмежень) складаємо для кожного стовпця таблиці постачань:

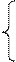
	х11 + х21 + … + хm1 = q1
	(3.3)
х1n + х2n + … + хmn = qn

Очевидно, що обсяг перевезеного вантажу не може бути від’ємним, тому слід додатково ввести обмеження: х_ij ≥ 0.

Ця задача може бути вирішена за допомогою симплекс-методу.

Властиві цій задачі специфічні особливості дозволяють отримати рішення більш простим способом шляхом заповнення спеціальної транспортної таблиці.

Особливості економіко-математичної моделі транспортної задачі:

- система обмежень являє собою систему лінійних рівнянь;

- коефіцієнти при перемінні системи обмежень рівні 1 і 0;

- кожна перемінна входить у систему обмежень два рази:

один раз - у систему рівнянь (3.2), і один раз - у систему рівнянь (3.3).