Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

W - 15x1 - 200x2 ≥ 0.

Зобразимо його прямою W:

W - 15x₁ - 200x₂ = 0. (2.4)

Мінімальне значення W прийме, якщо пряма, що її представляє, торкнеться ОПР у самій лівій її частині - у точці А чотирикутника ABCD. При збільшенні W (2.4) пряма переміщається вправо. Крапку торкання прямої W (2.4) можна визначити вирішивши систему рівнянь для
х₃ = 0 і х₅ = 0 з (2.3). У результаті одержуємо х₁ = 20 і х₂ = 2. Звідси випливає, що
W = 700. Координати крапки А (20; 2) і є рішенням задачі. У розглянутому випадку оптимальне рішення – єдине.

При W < 700 пряма W лежить поза ОПР, тобто жодна з її точок не є рішенням.

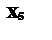
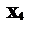
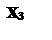
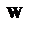
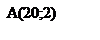
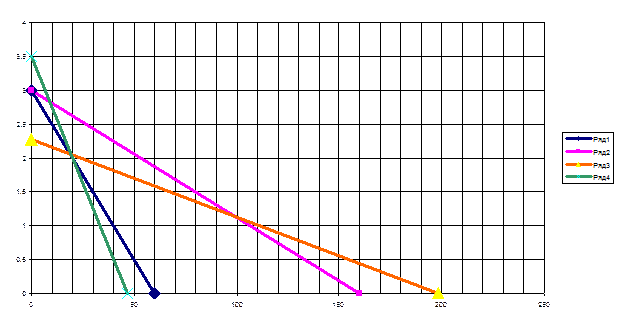Мал. 2.1.

Можливі й інші ситуації.

Якби пряма W збіглася з прямою AD, мі малі б нескінчену множину рішень відповідних крапкам, що лежати на відрізку AD (включаючи крапку А). З іншого боку, деякі задачі можуть і не мати рішення через несумісність обмежень (2.3) – для них відсутня ОПР.

У нашій задачі це могло вийти, наприклад, при виділенні дуже малого числа штатних одиниць чи надмірного збільшення території, що обслуговується, при незмінності інших вимог.

Зауважимо, що змінні х₁ і х₂ реально можуть мати тільки цілочислові рішення. У дійсності припустимі рішення відповідають дискретній множині крапок в ОПР. У подібних випадках точні рішення дають спеціальні методи ЛП.

Тема 3.