
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Механика твердого тела
|
|
В динамике вращательного движения твердого тела пользуются понятиями момента инерции 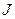 , момента силы
, момента силы 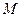 и момента импульса
и момента импульса  . Момент инерции материальной точки относительно некоторой оси есть скалярная величина, равная произведению массы точки на квадрат расстояния от нее до оси вращения.
. Момент инерции материальной точки относительно некоторой оси есть скалярная величина, равная произведению массы точки на квадрат расстояния от нее до оси вращения.
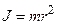
Моментом инерции тела относительно данной оси называется физическая величина, равная сумме произведений масс элементарных частей тела (точек) на квадрат их расстояний до этой оси
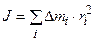
В случае непрерывного распределения масс сумма заменяется интегралом
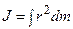
Применяя эти формулы, можно вычислить моменты инерции для некоторых тел, которые приведены ниже в таблице.
Если задана ось вращения, которая не проходит через центр инерции, то момент инерции относительно этой оси можно определить на основе теоремы Штейнера
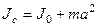
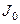 – момент инерции тела относительно оси, проходящей через центр масс;
– момент инерции тела относительно оси, проходящей через центр масс;
a – расстояние между осями.
 – момент инерции тела относительно произвольной оси равен моменту инерции его относительно оси, проходящей через центр тела и параллельно произвольной оси
– момент инерции тела относительно произвольной оси равен моменту инерции его относительно оси, проходящей через центр тела и параллельно произвольной оси 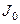 плюс произведение массы тела на квадрат расстояния между осями.
плюс произведение массы тела на квадрат расстояния между осями.
| Тело | Положение оси | Момент инерции |
| Полый тонкостенный цилиндр радиусом R | Ось симметрии | mR 2 |
| Сплошной цилиндр или диск радиусом R | Ось симметрии |  mR 2 mR 2
|
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через середину | 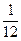 ml 2 ml 2
|
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его конец | 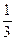 ml 2 ml 2
|
| Шар радиусом R | Ось проходит через центр шара | 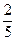 mR 2 mR 2
|
При вращательном движении момент инерции есть мера инертности тела.
Моментом силы 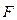 относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса – вектора
относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса – вектора 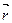 , проведенного из точки О в точку приложения силы, на силу
, проведенного из точки О в точку приложения силы, на силу  (рис.5).
(рис.5).
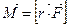 ,
,
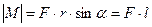
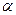 – угол между направлениями
– угол между направлениями  и
и 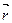
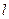 – плечо силы.
– плечо силы.
Направление момента силы определяется правилом правого винта.

рис.5
Момент импульса материальной точки относительно неподвижной точки О называется физическая величина, определяемая векторным произведением

где 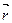 – радиус-вектор, проведенный из точки O к материальной точке.
– радиус-вектор, проведенный из точки O к материальной точке.
Модуль момента импульса
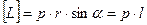
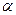 – угол между направлениями
– угол между направлениями 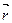 и
и 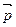
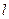 – плечо импульса
– плечо импульса 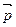 относительно точки О.
относительно точки О.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Направление момента импульса определяется по правилу правого винта.
Момент импульса твердого тела относительно оси 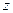 равен
равен
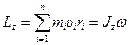
где 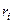 – расстояние от оси
– расстояние от оси 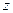 до отдельной частицы тела;
до отдельной частицы тела; 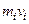 – импульс этой частицы;
– импульс этой частицы; 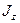 – момент инерции тела относительно оси
– момент инерции тела относительно оси 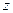 ;
; 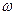 – его угловая скорость.
– его угловая скорость.
Основной закон вращательного движения: 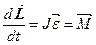
Если момент внешних сил, действующих на тело, равен нулю (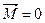 ), то
), то 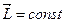 . Это выражение является законом сохранения момента импульса.
. Это выражение является законом сохранения момента импульса.
Кинетическая энергия вращающегося тела равна
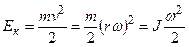
Изменение кинетической энергии тела определяется работой, совершаемой силой 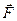 , которая равна произведению момента силы на угловой путь:
, которая равна произведению момента силы на угловой путь:

|
|
