
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основы механики
|
|
Механика изучает самый простой вид движения – механическое движение. Механическое движение – изменение с течением времени положения тела относительно других тел. Для изучения механического движения надо ввести систему отсчета: неподвижное тело отсчета и связанная с ним система координат.
В механике в зависимости от условий конкретных задач, применяются различные физические модели. Простейшей моделью является материальная точка – тело, обладающее массой, размерами которого можно пренебречь.
Произвольное макроскопическое тело или систему тел можно разбить на малые, взаимодействующие между собой части, каждая из которых рассматривается как материальная точка. Тогда изучение движения произвольной системы тел сводит к изучению системы материальных точек.
Тело, деформацией которого при взаимодействии с другими телами можно пренебречь, можно рассматривать как абсолютно твердое тело.
Сплошная среда – среда с непрерывно распределенным веществом.
Механика состоит из двух основных разделов: кинематики и динамики.
Кинематика – изучает движение тел, не рассматривая причины, которые вызывают или изменяют это движение.
Динамика – изучает законы движения тел и причины, которые вызывают или изменяют это движение.
Любое движение твердого тела можно представить как совокупность двух простых движений: поступательного и вращательного движений. Поступательное движение – это движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. При таком движении можно ограничиться рассмотрением одной точки тела, центра масс тела.
Вращательное движение – это движение, при котором все точки тела движутся по окружностям, центры которых лежат на прямой, называемой осью вращения.
В кинематике движение материальной точки описывается с помощью кинематических уравнений:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
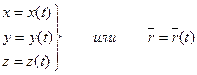
здесь, x, y, z – координаты точки, 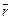 – радиус-вектор (см. рис.1)
– радиус-вектор (см. рис.1)
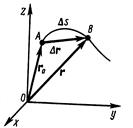
рис.1
Линия, описываемая материальной точкой в пространстве, называется траекторией движения. Траектория может представлять прямую линию (прямолинейное движение).
Кинематические величины:
1. Перемещение – вектор, соединяющий начальное и последующее положение материальной точки. На рис.1 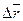 – перемещение из положения 1 в положение 2, совпадает с изменением радиус-вектора.
– перемещение из положения 1 в положение 2, совпадает с изменением радиус-вектора.
- Путь – длина траектории.
- Скорость – векторная величина, определяющая быстроту перемещения тела во времени.
В физике различают мгновенную и среднюю скорости.
Мгновенная скорость – векторная величина, равна 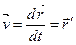 и определяется первой производной радиус-вектора тела по времени, направлена по касательной к траектории. Модуль мгновенной скорости равен первой производной пути по времени:
и определяется первой производной радиус-вектора тела по времени, направлена по касательной к траектории. Модуль мгновенной скорости равен первой производной пути по времени: 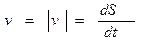
Если мы знаем закон изменения  за некоторый промежуток времени
за некоторый промежуток времени  , то сможем определить пройденный путь за
, то сможем определить пройденный путь за 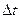 :
:
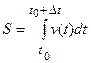
Средняя скорость – векторная величина, равная отношению приращения радиус-вектора 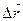 к промежутку времени
к промежутку времени 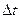 :
:
 .
.
Модуль средней скорости равен расстоянию за единицу времени:
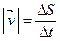
Ускорение – векторная величина, характеризующая изменение скорости тела со временем, и равная первой производной от скорости по времени, т.е. 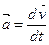
Среднее ускорение за некоторый промежуток времени 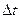
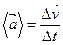 , где
, где 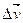 – изменение скорости за
– изменение скорости за 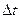 .
.
Ускорение можно представить в виде векторной суммы двух слагаемых (рис.2)

Первое слагаемое характеризует изменение скорости по модулю и называется тангенциальной составляющей (касательной) ускорения.
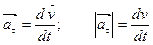
Второе слагаемое характеризует изменение скорости по направлению и называется нормальным ускорением.

где R – радиус кривизны. Если материальная точка движется по окружности то R – радиус окружности.
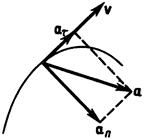
рис.2
В случае прямолинейного равномерного движения
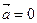
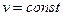 и путь
и путь 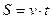
При прямолинейном равнопеременном движении

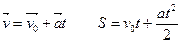
здесь 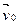 – скорость тела в момент времени
– скорость тела в момент времени 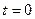 ; а > 0, если тело движется равноускоренно, и а < 0 при равнозамедленном движении тела.
; а > 0, если тело движется равноускоренно, и а < 0 при равнозамедленном движении тела.
При равномерном движении материальной точки по окружности  ,
,  .
.
Для описания вращательного движения макроскопического тела используют величины: угловой путь 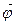 , угловую скорость
, угловую скорость  , угловое ускорение
, угловое ускорение  (рис.3):
(рис.3):
Модуль вектора углового пути равен углу поворота 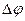 .
.
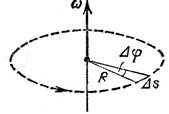
рис.3
Угловая скорость – векторная величина, определяемая первой производной углового пути тела по времени и характеризующая быстроту изменения угла поворота.

Направление векторов угловой скорости и углового пути совпадают и определяются правилом правого винта.
Угловое ускорение – векторная величина, определяемая первой производной угловой скорости по времени:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе

При равнопеременном вращении тела вокруг некоторой оси

где 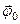 и
и 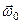 – начальные значения углового пути и угловой скорости соответственно.
– начальные значения углового пути и угловой скорости соответственно.
Линейные кинематические величины связаны с угловыми.
Зная угловые величины 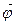 ,
, 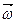 ,
,  , можно найти
, можно найти 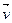 и
и  , воспользовавшись следующими формулами:
, воспользовавшись следующими формулами:
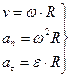 , здесь R – радиус окружности.
, здесь R – радиус окружности.
|
|
