Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Б) Уравнение Шредингера. Волновая функция

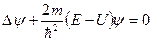– стационарное уравнение Шредингера;

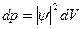– вероятность обнаружить частицу в объеме dV;

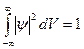– условие нормировки волновой функции;

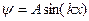– решение уравнения Шредингера для частицы в одномерном потенциальном ящике с бесконечно высокими стенками,

где

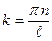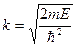; – модуль волнового вектора;

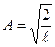– амплитуда волновой функции;

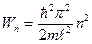– энергия частицы в одномерном потенциальном ящике с бесконечно высокими стенками, где n – квантовое число, принимающее значения: n =1, 2, 3…

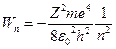– полная энергия электрона в атоме водорода, где n – главное квантовое число, принимающее значения n =1, 2, … ∞;

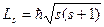– спиновый (собственный) момент импульса (механический момент) электрона в атоме водорода, где s – спиновое квантовое число, s =1/2;

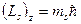– проекция механического спинового момента электрона в атоме водорода на выделенное направление, где m_s – магнитное квантовое число, принимающее значения: m_s =±1/2;

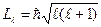– орбитальный момент импульса (механический момент) электрона в атоме водорода, где 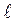– орбитальное квантовое число, принимающее значения:

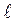=0, 1, 2 … n –1;

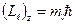– проекция механического орбитального момента электрона в атоме водорода на выделенное направление, где 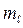– магнитное квантовое число, принимающее значения: 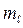=0, ±1, ±2, … ± ;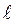