Энергетический критерий устойчивости целиков

В рассмотренных схемах расчета прочных размеров целиков имеется ряд нереальных допущений. Наиболее важными из них являются следующие:

1. Нагрузка на целик принимается независящей от деформации целика, кровли и почвы.

2. Принимается, что разрушение целика наступает, когда среднее или среднее эффективное напряжение в нем достигаем временного сопротивления целика сжатию.

Независимость нагрузки на целик от его деформации может иметь место лишь при обширной отработанной площади и большом числе целиков.

Влияние деформационных свойств целика, кровли и почвы на нагрузку на целик может быть легко показано, если целик заменить сильным домкратом (рис.52), оказывающим реакцию F_j на почву и кровлю.

Если домкрат постепенно опускать, конвергенция кровли и почвы будет возрастать; опорная нагрузка кровли на массив F_a будет увеличиваться, а нагрузка на домкрат F_j будет уменьшаться. Скорость снижения нагрузки на целик при росте конвергенции зависит от деформативной способности кровли, ночвы и массива в опорах. График разгрузки целика-домкрата будет иметь вид, показанный на рис. 52. Чем выше жесткость кровли, почвы и опор, тем круче наклон кривой разгрузки. Площадь под наклонной кривой представляет собой энергию, выделяемую массивом при конвергенции кровли и почвы.

Рис. 52. Аналогия домкрата и целика:

F_a- опорная нагрузка на массив; F_j – нагрузка на целик;

δ /2 – конвергенция кровли и почвы

Рис. 53. График разгрузки кровли

Если прочность кровли настолько велика, что она может допустить пролет JM (см. рис.52) не разрушаясь, то целик-домкрат можно будет разгрузить полностью и всю нагрузку пород кровли передать на опоры. Белее вероятно, что при некоторой величине спускания домкрата, начнется отслоение пород кровли в контуре, показанном на рис.52 пунктиром.

Отслаивающаяся порода передает свой вес на целик (пунктирная линия на рис.53). Этот вес, очевидно, будет намного меньше полного веса столба пород в пролете JM до поверхности.

Таким образом, нагрузка на целик находится в прямой зависимости от величины конвергенции и деформативных свойств целика, кровли, почвы и опор.

Нереальность второго допущения вытекает из первого. Полное разрушение целика наступает лишь при условии, если нагрузка на него будет постоянно превосходить реакцию целика при его деформации. График полной кривой «реакция-деформация» для целика приведен на рис. 54. Площадь под кривой ОАВС представляет собой энергию, поглощаемую целиком при его деформации. Подъем кривой на участке ОА и падение на участке AВC зависят от материала целика, его формы, отношения высоты к ширине и других факторов.

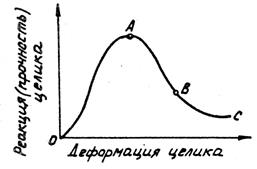
Рис. 54. Зависимость реакции целика от его деформации

Пока несущая способность целика возрастает с деформацией (участок ОА рис.54) целик будет устойчив. При деформации на участке ABC устойчивость целика будет определяться соотношением скорости падения несущей способности целика и скорости снижения нагрузки на целик со стороны кровли с величиной конвергенции. Это соотношение показано на рис.55. Если величина нагрузки со стороны кровли при конвергенции изменяется по линии PR_u, a несущая способность целика изменяется по линии PQ (касательная в точке Р), то выделяемая энергия за точкой P превышает энергию, которую может адсорбировать (поглотить) целик и целик будет неустойчивым. Дальнейшее превышение выделяемой энергии над поглощаемой целиком приведет к его быстрому разрушению. Если разгрузка пород кровли (почвы) будет идти по линии PR_s, целик будет устойчивым, хотя и частично разрушенным. Энергия, выделяемая массивом при конвергенции, меньше энергии, которую способен поглотить целик, поэтому дальнейшая конвергенция пород не будет иметь места.

Выемка полезного ископаемого за пределами опор приведет к дополнительной конвергенции пород над целиком (на рис.68, бточка Р переместится в точку Р'). Так как нагрузка теперь превышает несущую способность целика, произойдет его дальнейшая деформация по линии РТ. Это приведет к снижению нагрузки на целик по линии Р'Т. Выделенная энергия пойдет на дополнительное разрушение целика, однако это не приведет к его полному разрушению. Начиная с точки Т, состояние целика вновь станет устойчивым. Таким образом, допущение о том, что для полного разрушения целика достаточным является условие, когда среднее или среднее эффективное напряжение в нем достигает величины временного сопротивления материала сжатию, является неверным.

Условия устойчивости целика в общем виде могут быть сформулированы на основе известного в механике выражения условия устойчивости системы

.

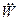– вариация второго рода от полной потенциальной энергии системы;

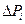– дополнительные небольшие нагрузки в различных точках системы;

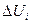– дополнительные смещения в системе, вызванные нагрузками .

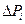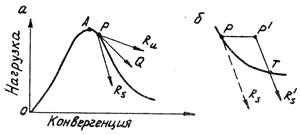
Рис. 55. Критерий устойчивости целика

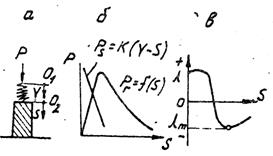
Рис. 56. Работа породного образца в испытательной машине:

а – схема погружения; б – деформационные характеристики машины и образца; в – зависимость жесткости образца от его деформации

В качестве аналога работы целика рассмотрим поведение породного образца в обычной испытательной машине (рис.56, а). На рис.56, б приведены кривые «напряжение-деформация» для испытательной машины и породного образца. Эти зависимости могут быть представлены в виде:

– для испытательной машины (пружины) – ;

– для породного образца – .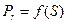

Для сохранения равновесия необходимо иметь

.

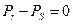Проверим условие устойчивости системы путем приложения в точке О ₂ (рис.56, а) небольшой внешней силы, вызывающей деформацию 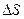. Тогда изменения усилий в породном образце и машине будут

;

.

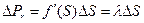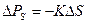И, следовательно,

,

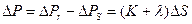где 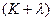– может рассматриваться как эффективная жесткость системы «машина-образец». Критерием устойчивости является выражение

,

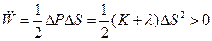что выполняется при условии .

Вмещающие породы выполняют роль машины (пружины) с локальной жесткостью К_li, целик с жесткостью λ _i выполняет роль породного образца. Условие устойчивости выразится в виде

Величина К_li всегда положительна, величина λ _i положительна в области упругой и упругопластической (до величины временного сопротивления) деформации целика и отрицательна в запредельной области. Поэтому неустойчивое состояние целика может наступить только при его работе в запредельной области, если

Жесткость целиков в запредельной области изучена мало. Необходимы дальнейшие исследования.