Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Закон Джоуля-Ленца в дифференцированной и интегральной форме

Опытом установлено, что если в проводнике течет ток, то работа сторонних сил расходуется на его нагревание. Предполо­жим, что на концах участка проводника имеется разность потен­циалов U = φ ₁ – φ ₂.

Тогда работа по переносу заряда Q на этом участке равна

A = Q (φ ₁ – φ ₂) = QU.

Если ток постоянный, то

и

A = I · U · t.

Эта работа равна количеству теплоты Q, и формула Q = I · U · t вы­ражает закон Джоуля-Ленца в интегральной форме.

Используя выражение закона Ома получим

.

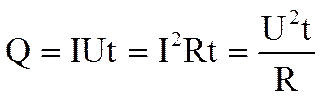Преобразуем закон Джоуля–Ленца. Введем плотность тепловой мощности w – величину, равную энергии, выделяемой за время t прохождения тока в единице объема проводника:

,

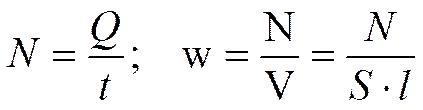
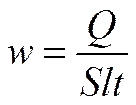где S - сечение, l - длина проводника. Подставляя Q = I² R t и 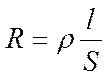, получим .

Здесь 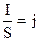- плотность тока, 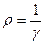, и учитывая, что j = γ E, получим

.

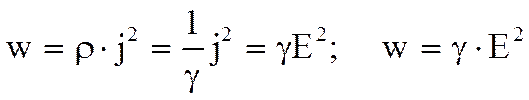Это есть выражение закона Джоуля-Ленца в дифференциальной форме. Плотность тепловой мощности в проводнике, по которому течет ток, прямо пропорциональна квадрату напряженности поля в проводнике. Коэффициентом пропорциональности является удель­ная проводимость проводника.

Вывод законов Ома и Джоуля-Ленца из классических электрон­ных представлений

Какова природа носителей тока в металлах? В 1901 г. Рикке проделал опыты: через 3 цилиндра, установленных друг на друга в течение 3-х лет пропускал постоянный ток. Был пропущен заряд, равный 3, 5 ·10⁶ Кл. Взвешивание показало неизменный вес цилинд­ров. Исследование торцов цилиндров не показало следов переноса вещества. Из этого был сделан вывод, что носители заряда не ионы, а открытые Томпсоном в 1897 г. электроны.

Чтобы отождествить носители заряда с электронами, нужно было определить знак и величину удельного заряда носителей.

Если в металле имеются легко перемещающиеся заряженные частицы, то при торможении металлического проводника эти час­тицы должны некоторое время продолжать двигаться по инерции, в результате чего в проводнике возникнет импульс тока и будет пе­ренесен некоторый заряд.

Мандельштам и Папалекси в 1913 г. проделали такой опыт – они приводили в быстрое крутильное колебание катушку с прово­дом вокруг ее оси. К концам катушки подключили телефон, в кото­ром был слышен звук, обусловленный импульсами тока. Был полу­чен качественный результат – зарегистрирован импульс тока.

Толмен и Стюарт в 1916 г. получили количественный ре­зультат. Катушка с проводом длиной 500 м приводилась во враще­ние со скоростью v=300 м/с. Катушка резко тормозилась и с по­мощью баллистического гальванометра измеряли заряд, протекав­ший в цепи во время торможения. Вычисленное значение отношения заряда к массе e/m полу­чалось очень близким для электронов. Таким образом было доказано, что носителем тока являются электроны. Исходя из представлений о свободных электронах была создана классическая теория электро­проводности металлов в предположении, что:

- электроны в металле ведут себя подобно молекулам иде­ального газа;

- движение электронов подчиняется законам классической механики;

- взаимодействие электронов сводится к соударениям с ио­нами кристаллической решетки;

- силами взаимодействия между электронами можно пре­небречь и они между собой не сталкиваются;

- электроны в отсутствие электрического поля движутся хаотически.

Вычислим плотность тока j в проводнике, возникающего под действием поля напряженностью Е.

По определению плотность тока j = n·e·< v> - это заряд, переносимый через единицу площади S = 1м² за единицу времени t=1 с; n – концентрация электронов, е – заряд элек­трона, ·< v> - средняя скорость упорядоченного движения электро­нов.

На каждый электрон действует сила F = eE = ma, поэтому электрон приобретает ускорение и к концу свободного про­бега он достигнет скорости

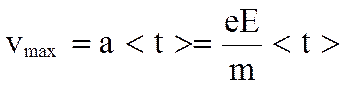, а средняя скорость

< v> =v_max/2

Если < v_T> - средняя скорость теплового хаотичного движе­ния электронов, а средняя длина свободного пробега электронов < λ >, то среднее время между соударениями < t> = 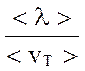. Подставляя < t> в формулу для < v> получим:

.

Подставляя < v> в формулу для j, получим

,

т.е. плотность тока прямо пропорциональна Е, а это и есть выраже­ние закона Ома в дифференциальной форме. Если положить, ч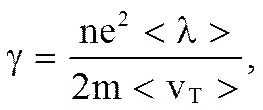то

то

j = γ E.

Удельная проводимость γ ~ n и < λ >, < v_т> ~ T, поэтому проводимость снижа­ется с ростом температуры, а удельное сопротивление 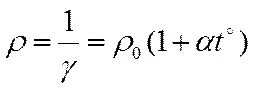по­вышается с ростом температуры. К концу свободного пробега электрон приоб­ретает кинетическую энергию

Предполагается, что вся энергия при соударении передается узлу кристаллической решетки и переходит в тепло. За 1 с электрон ис­пытывает < v_T> / < λ > cоударений, а значит выделяет во столько же раз больше тепла. Если в единице объема n электронов, то в еди­нице объема за единицу времени выделится количество тепла

.

Таким образом, - выражение закона Джоуля-Ленца в дифференциальной форме.

Закон Видемана-Франца. Затруднения классической электрон­ной теории

Известно, что металлы наряду с высокой электропроводностью обладают также большой теплопроводностью. Видеман и Франц в 1853 г. эмпирически установили закон: отношение коэффициента теплопроводности χ к коэффициенту электропроводности γ для всех металлов приблизительно одинаково и прямо пропорционально аб­солютной температуре

.

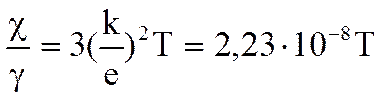Таким образом, классическая электронная теория хорошо объясняет существование электрического сопротивления металлов, законы Ома и Джоуля-Ленца, позволяет выразить удельную тепло­проводность через атомарные постоянные металла, объясняет зави­симость электропроводности от температуры и позволяет понять связь между теплопроводностью и электропроводностью металлов.

Однако в некоторых вопросах, классическая электронная теория приходит к выводам, находящимся в противоречии с опы­том.

1. Исходя из классической электронной теории удельная электропроводность равна

,

откуда

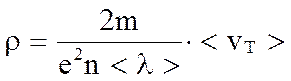, но ,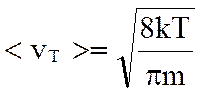

т.е. < v_T> ∼ .

Следовательно, по теории ρ ∼ , тогда как на практике

,

т.е. удельное сопротивление пропорционально первой степени тем­пературы Т.

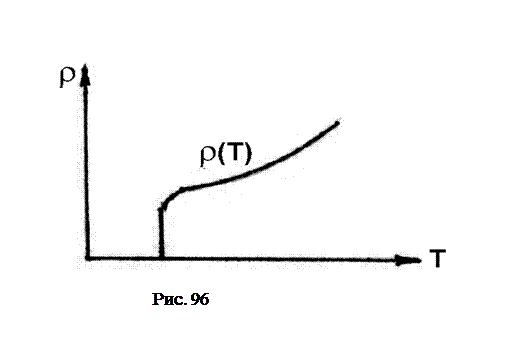
Кроме того, согласно классической электронной теории удельное сопротивление ρ должно монотонно уменьшаться при охлаждении, оставаясь при всех температурах по значению конечным. Это и наблюдается при сравнительно высоких температурах. Однако при достаточно низ­ких температурах удельное сопротивление перестает зависеть от температуры и достигает некоторого предельного значения, кото­рое называют остаточным сопротивлением (велико у сплавов, су­ществует у чистых металлов и тем меньше, чем чище металл и меньше структурных дефектов).

Если понижать температуру еще ниже, то в некоторых веществах наблюдается явление сверхпроводи­мости, т.е. удельное сопротивление внезапно скачком уменьшается прак­тически до нуля (рис. 96). В сверхпро­водниках однажды возбужденный электрический ток может длительно существовать без источника тока (в течение нескольких суток). В таком состоянии не выполняется за­кон Ома.

2. Другим затруднением классической электронной теории металлов может служить теория теплоемкости кристаллов. Со­гласно этой теории “электронный газ” металлов должен обладать молярной теплоемкостью . Добавляя эту теплоемкость к тепло­емкости кристаллической решетки, составляющей 3R, получим для молярной теплоемкости металла значение (9/2)R. Таким образом, согласно классической электронной теории молярная теплоемкость металла должна быть в 1, 5 раза выше, чем у диэлектриков. Однако на практике их молярные теплоемкости практически не различа­ются. Объяснение этих различий и явлений дается в рамках кванто­вой теории металлов.

В классической теории неверным является предположение, что электроны проводимости подчиняются законам статистики Максвелла-Больцмана и что для них справедлив закон распределе­ния энергии Максвелла. На самом деле они подчиняются законам квантовой статистики и закону распределения энергий Ферми-Ди­рака.

Энергия электронов в металлах слабо зависит от темпера­туры и теплоемкость электронного газа оказывается близка к нулю, поэтому наличие электронного газа в металлах практически не ска­зывается на теплоемкости.

Далее, в классической электронной теории не учитывается взаимодействие электронов друг с другом, а их взаимодействие с решеткой металла описывается с помощью представления о соуда­рениях. При низких температурах взаимодействие между электро­нами начинает играть решающую роль. Кроме того, оказалось, что взаимодействие электронов с решеткой имеет иной характер – электроны движутся в периодическом поле электрического потен­циала решетки.

И, наконец, движение электронов в металлах подчиняется законам квантовой, а не классической механики.