Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!
Задание 16
|
|
С помощью определенного интеграла найти:
16.1 Объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной параболами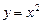 
и 
.
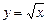16.2 Объем тела, полученного вращением вокруг оси Оу фигуры, ограниченной кривым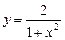и 
и .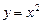
16.3 Объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной кривой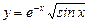 
, 
.
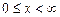16.4 Объем тела, полученного вращением вокруг оси Оу фигуры, ограниченной линиями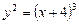 
, х=0.
16.5 Объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной линиями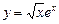 
, х=1, у=0.
16.6 Объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной кривой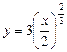 
, 
.
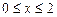16.7 Объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной одной дугой синусоиды y=sinx и осью Ох.
16.8 Объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной кривой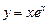 
и прямыми у=0, х=1.
16.9 Объем тела, полученного вращением криволинейной трапеции, ограниченной линией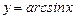 
с основанием [0, 1], вокруг оси Ох.
16.10 Объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной линиями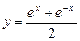 
, х=a, х=b.
16.11 Фигура, ограниченная гиперболой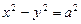 
и прямой х=a+2, вращается вокруг оси Ох. Найти объем тела вращения.
16.12 Объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной линиями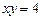 
, у=0, х=1, х=4.
16.13 Объем тела, полученного вращением вокруг оси Ох астроиды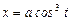 
, 
.
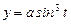16.14 Объем тела, полученного вращением вокруг оси Ох фигуры, ограниченной линиями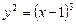 
, х=2.
16.15 Объем тела, образованного вращением вокруг оси Ох кривой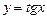 
, 
.
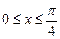16.16 Объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной циссоидой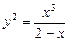 
и прямой х=1.
16.17 Объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной линиями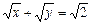 
, х=0, у=0.
16.18 Объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной линиями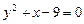 
, х=0.
16.19 Объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной цепной линией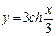 
, осью Ох и прямыми х=±3.
16.20 Объем тела, образованного вращением вокруг оси Оу эллипса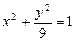 
.
16.21 Объем тора, образованного вращением вокруг оси Ох круга
.
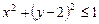16.22 Объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиям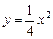и 
и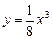 
.
16.23 Объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной линиям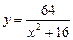и 
и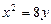 
.
16.24 Объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной петлей криво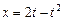й 
и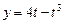 
.
16.25 Объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной полуэллипсом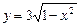 
, параболой 
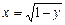и осью Оу.
ЛИТЕРАТУРА
1. Фихтенгольц, Г.М. Основы математического анализа / Г.М. Фихтенгольц. – М.: Наука, 1968.
2. Дюбюк, П.Е. Сборник задач по курсу высшей математики / П.Е. Дюбюк, Г.И. Кручкович.– М.: Высшая школа, 1965.
3. Данко, П.Е. Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов. – М.: Высшая школа, 1986.
Учебное издание
Ростова Ольга Дмитриевна
Тушкина Татьяна Михайловна
|
|