💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

ЗАДАНИЕ 1. Применяя метод интегрирования по частям, найти:

Применяя метод интегрирования по частям, найти:

1.1 ;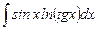

1.2 ;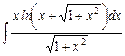

1.3 ;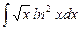

1.4 ;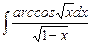

1.5 ;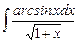

1.6 ;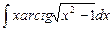

1.7 ;

1.8 ;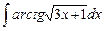

1.9 ;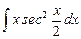

1.10 ;

1.11 ;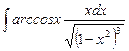

1.12 ;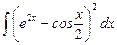

1.13 ;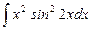

1.14 ;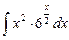

1.15 ;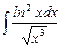

1.16 ;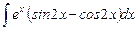

1.17 ;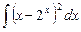

1.18 ;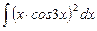

1.19 ;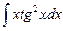

1.20 ;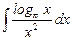

1.21 ;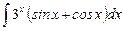

1.22 ;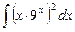

1.23 ;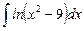

1.24 ;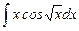

1.25 .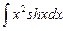

ЗАДАНИЕ 2

Найти интегралы от рациональных дробей:

2.1 ;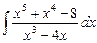

2.2 ;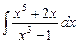

2.3 ;

2.4 ;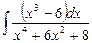

2.5 ;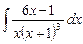

2.6 ;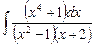

2.7 ;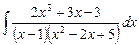

2.8 ;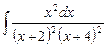

2.9 ;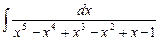

2.10 ;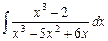

2.11 ;

2.12 ;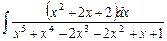

2.13 ;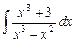

2.14 ;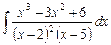

2.15 ;

2.16 ;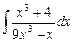

2.17 ;

2.18 ;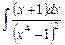

2.19 ;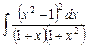

2.20 ;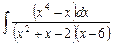

2.21 ;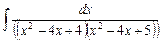

2.22 ;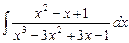

2.23 ;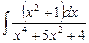

2.24 ;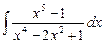

2.25 .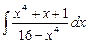

ЗАДАНИЕ 3

Найти интегралы от иррациональных функций:

3.1 ;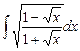

3.2 ;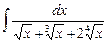

3.3 ;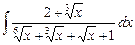

3.4 ;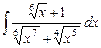

3.5 ;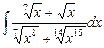

3.6 ;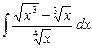

3.7 ;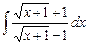

3.8 ;

3.9 ;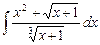

3.10 ;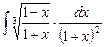

3.11 ;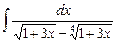

3.12 ;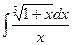

3.13 ;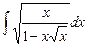

3.14 ;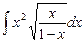

3.15 ;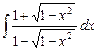

3.16 ;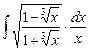

3.17 ;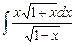

3.18 ;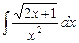

3.19 ;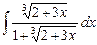

3.20 ;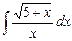

3.21 ;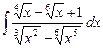

3.22 ;

3.23 ;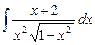

3.24 ;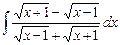

3.25 .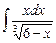

ЗАДАНИЕ 4

Найти интеграл от дифференциального бинома:

4.1 ;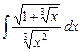

4.2 ;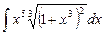

4.3 ;

4.4 ;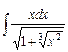

4.5 ;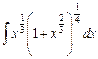

4.6 ;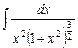

4.7 ;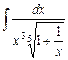

4.8 ;

4.9 ;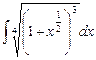

4.10 ;

4.11 ;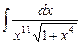

4.12 ;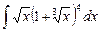

4.13 ;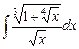

4.14 ;

4.15 ;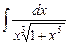

4.16 ;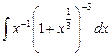

4.17 ;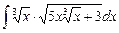

4.18 ;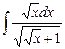

4.19 ;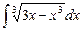

4.20 ;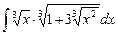

4.21 ;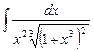

4.22 ;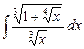

4.23 ;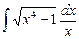

4.24 ;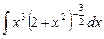

4.25 .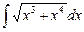

ЗАДАНИЕ 5

Применяя подстановки Эйлера, найти:

5.1 ;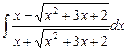

5.2 ;

5.3 ;

5.4 ;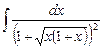

5.5 ;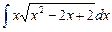

5.6 ;

5.7 ;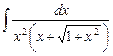

5.8 ;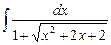

5.9 ;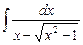

5.10 ;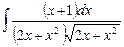

5.11 ;

5.12 ;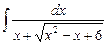

5.13 ;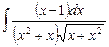

5.14 ;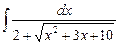

5.15 ;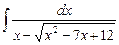

5.16 ;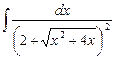

5.17 ;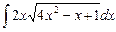

5.18 ;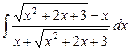

5.19 ;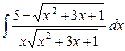

5.20 ;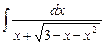

5.21 ;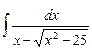

5.22 ;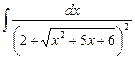

5.23 ;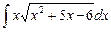

5.24 ;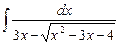

5.25 .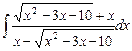

ЗАДАНИЕ 6

Найти:

6.1 ;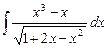

6.2 ;

6.3 ;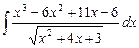

6.4 ;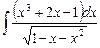

6.5 ;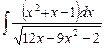

6.6 ;

6.7 ;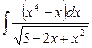

6.8 ;

6.9 ;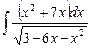

6.10 ;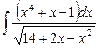

6.11 ;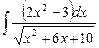

6.12 ;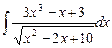

6.13 ;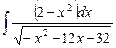

6.14 ;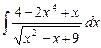

6.15 ;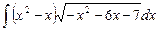

6.16 ;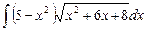

6.17 ;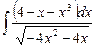

6.18 ;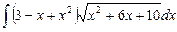

6.19 ;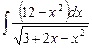

6.20 ;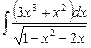

6.21 ;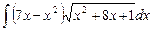

6.22 ;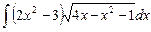

6.23 ;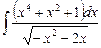

6.24 ;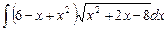

6.25 .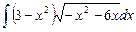

ЗАДАНИЕ 7

Найти интегралы от тригонометрических функций:

7.1 ;

7.2 ;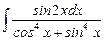

7.3 ;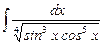

7.4 ;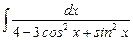

7.5 ;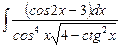

7.6 ;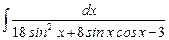

7.7 ;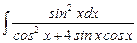

7.8 ;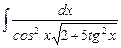

7.9 ;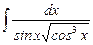

7.10 ;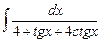

7.11 ;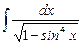

7.12 ;

7.13 ;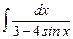

7.14 ;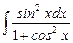

7.15 ;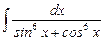

7.16 ;

7.17 ;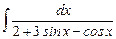

7.18 ;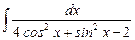

7.19 ;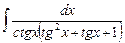

7.20 ;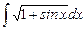

7.21 ;

7.22 ;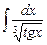

7.23 ;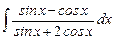

7.24 ;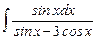

7.25 .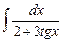

ЗАДАНИЕ 8

Найти интегралы от гиперболических функций:

8.1 ;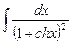

8.2 ;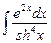

8.3 ;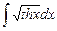

8.4 ;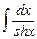

8.5 ;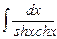

8.6 ;

8.7 ;

8.8 ;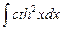

8.9 ;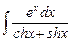

8.10 ;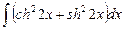

8.11 ;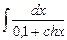

8.12 ;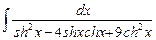

8.13 ;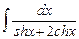

8.14 ;

8.15 ;

8.16 ;

8.17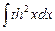

8.18 ;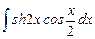

8.19 ;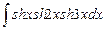

8.20 ;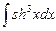

8.21 ;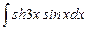

8.22 ;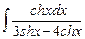

8.23 ;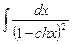

8.24 ;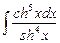

8.25 .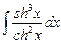

ЗАДАНИЕ 9

Найти интегралы от трансцендентных функций:

9.1 ;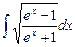

9.2 ;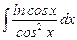

9.3 ;

9.4 ;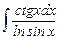

9.5 ;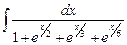

9.6 ;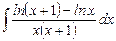

9.7 ;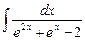

9.8 ;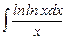

9.9 ;

9.10 ;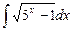

9.11 ;

9.12 ;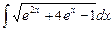

9.13 ;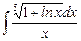

9.14 ;

9.15 ;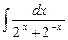

9.16 ;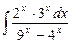

9.17 ;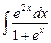

9.18 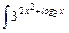dx;

9.19 ;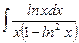

9.20 ;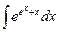

9.21 ;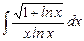

9.22 ;

9.23 ;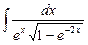

9.24 ;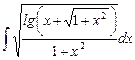

9.25 .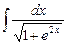

ЗАДАНИЕ 10

Вычислить, пользуясь формулой Ньютона–Лейбница:

10.1 ;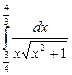

10.2 ;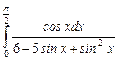

10.3 ;

10.4 ;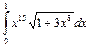

10.5 ;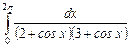

10.6 ;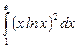

10.7 ;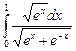

10.8 ;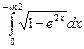

10.9 ;

10.10 ;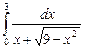

10.11 ;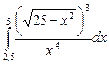

10.12 ;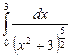

10.13 ;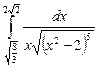

10.14 ;

10.15 ;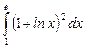

10.16 ;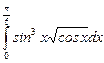

10.17 ;

10.18 ;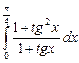

10.19 ;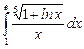

10.20 ;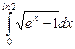

10.21 ;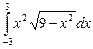

10.22 ;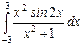

10.23 ;

10.24 ;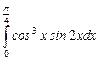

10.25 .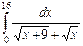

ЗАДАНИЕ 11

Исследовать на сходимость несобственные интегралы первого рода:

11.1 ;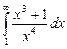

11.2 ;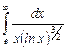

11.3 ;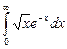

11.4 ;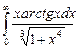

11.5 ;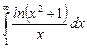

11.6 ;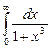

11.7 ;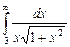

11.8 ;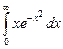

11.9 ;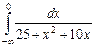

11.10 ;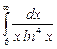

11.11 ;

11.12 ;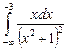

11.13 ;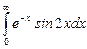

11.14 ;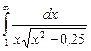

11.15 ;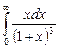

11.16 ;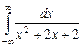

11.17 ;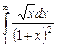

11.18 ;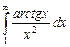

11.19 ;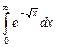

11.20 ;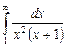

11.21 ;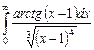

11.22 ;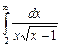

11.23 ;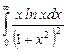

11.24 ;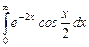

11.25 .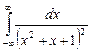

ЗАДАНИЕ 12

Исследовать на сходимость несобственные интегралы второго рода:

12.1 ;

12.2 ;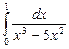

12.3 ;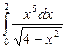

12.4 ;

12.5 ;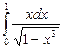

12.6 ;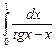

12.7 ;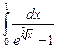

12.8 ;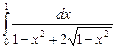

12.9 ;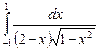

12.10 ;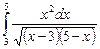

12.11 ;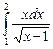

12.12 ;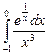

12.13 ;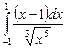

12.14 ;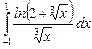

12.15 ;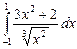

12.16 ;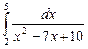

12.17 ;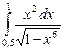

12.18 ;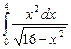

12.19 ;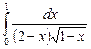

12.20 ;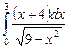

12.21 ;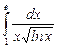

12.22 ;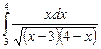

12.23 ;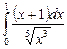

12.24 ;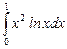

12.25 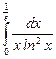.