
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Снесение координат с вершин знака на землю.
|
|
Снесение координат с вершин знака на землю.
Прямая засечка.
Обратная засечка.
Линейная засечка.
Рекомендуемая литература: [1], гл. XV, §§159–163; [11], гл. XV, §§123–129; [21], §129; [24], гл. 16, §§16.2–16.3; [27], гл. 11, §§105–106; [30], гл. VIII, §§51–52; [31], гл. VII, задание VII.5.
Снесение координат с вершин знака на землю.
Дополнительные пункты определяются наряду со съемочной сетью в основном для сгущения существующей геодезической сети пунктами съемочного обоснования. Они строятся прямыми, обратными, комбинированными угловыми, а при наличии электронных дальномеров – линейными засечками и лучевым методом.
В некоторых случаях дополнительный пункт определяется передачей (снесением) координат с вершины знака на землю.
При привязке полигонометрического (теодолитного) хода к пункту триангуляции, на котором нельзя установить прибор, выбирают на земле вблизи этого пункта А (на расстоянии 50–100 м от него) точку Р в таком месте, чтобы, кроме пункта А были видны два удаленных пункта исходной сети В и С (один из них необходим для контроля) и удобно было измерить два базиса для определения неприступного расстояния АР (рис. 2.19).

Рис. 2.19.
Для решения задачи измеряют базисы b и b ' и шесть углов β 1, β 2, β '1, β '2, δ и δ ' причем второй базис и углы при нем используют для контроля определения расстояния АР и повышения точности получения окончательного его значения, а угол δ ' – для контроля правильности произведенных измерений, выписки исходных данных и повышения точности определения окончательных значений координат точки Р (если их получают по результатам решений двух вариантов задачи).
Рассмотрим решение задачи по этапам.
1. Вычисление дирекционных углов (АВ), (АС) и расстояний АВ=s, AC = s '.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Имея координаты пунктов А и В, вычисляют дирекционный угол (АВ)
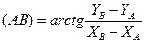 (1)
(1)
и расстояние АВ = s
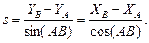 (2)
(2)
Если полученные значения s различаются на две единицы последнего знака, то за окончательное принимают среднее арифметическое.
Точно так же определяют дирекционный угол (АС) и расстояние АС. Иногда дирекционные углы (АВ), (АС) и расстояния АВ, АС не приходится вычислять, так как они бывают известны из материалов исходной геодезической сети.
2. Вычисление расстояния АР=d.
Недоступное расстояние АР = d определяют дважды:
 и
и 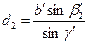 , (3)
, (3)
где γ = 1800 – (β 1 + β 2), γ ' = 1800 – (β '1 + β '2).
Разность | d 1 – d 2| не должна превышать 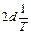 , где
, где 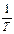 – предельная относительная погрешность измерения базисов b и b '.
– предельная относительная погрешность измерения базисов b и b '.
За окончательное значение расстояния АР принимают среднее арифметическое значение
 (4)
(4)
3. Вычисление дирекционного угла (AP).
Решая треугольники ABP и ACP, находят
 и
и  (5)
(5)
Затем вычисляют вспомогательные углы φ и φ '
φ = 1800 – (δ + ψ), φ ' = 1800 – (δ ' + ψ '). (6)
По этим углам определяют два значения дирекционного угла (AP)
(AP)1= (АВ) + φ, (AP)2= (АС) – φ '. (7)
Расхождение между значениями (АР)1и(АР)2должноудовлетворять неравенству
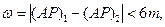 (8)
(8)
где m – средняя квадратическая погрешность измерения угла.
4. Вычисление координат точек P
По расстоянию AP = d и дирекционному углу (АР) находят, приращения координат
 (9)
(9)
Затем вычисляют координаты точки Р
 (10)
(10)
Полученные из двух решений значения координат не должны различаться больше, чем на величину 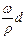 .
.
За окончательные значения координат принимают средние арифметические значения

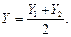 (11)
(11)
5. Оценка точности положения точки Р. Средней квадратической ошибкой положения точки называется средняя величина смещения относительно ее точного положения и определяемая в общем случае соотношением
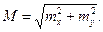 (12)
(12)
В данном случае средняя квадратическая ошибка положения точки Р может быть получена приближенно по формуле
 (13)
(13)
|
|
