Определение истинной величины углов

Задачу на определение истинной величины углов (плоских) удобнее решать путем преобразования исходного чертежа способом вращения вокруг линии уровня. Истинная величина углов между пересекающимися прямыми с и d (рис. 143) определена следующим образом: плоскость угла повернута вокруг своей фронтали f (1, 2) до совмещения ее с фронтальной плоскостью уровня Ф (Ф₁), проходящей через

Рис. 143

фронталь f Проекция MI совмещения вершины М угла между прямыми с и d находится на проекции Sum 2 фронтально проецирующей плоскости Sum, в которой вращается точка М. Определив с помощью прямоугольного треугольника О₂М₂М натуральную величину радиуса вращения r и отложив ее на проекции Е₂ от фронтальной проекции центра вращения, получаем изображение точки М на плоскости П₂в совмещенном с плоскостью Ф положении. Соединяя фронтальные проекции неподвижных точек 1 и 2 с построенной точкой М, получаем проекции с₂ и d₂, совмещенных с плоскостью Ф прямых с и d. Угол между прямыми с₂ и d₂ определяет натуральную величину искомого угла между пересекающимися прямыми с и d.

Эта задача также может быть решена способом замены плоскостей проекций. Для этого двойной заменой плоскостей проекций нужно сделать плоскость угла плоскостью уровня, решив последовательно сначала третью исходную задачу, а затем — четвертую.

Натуральная величина угла между скрещивающимися прямыми определяется как угол между двумя пересекающимися прямыми, параллельными данным скрещивающимся прямым.

Угол а между прямой l и плоскостью 6 может быть определен через дополнительный угол р между заданной прямой l и перпендикуляром п к данной плоскости, проведенной из любой точки прямой (рис. 144). Угол Р дополняет искомый угол а до 90°. Определив истинную величину угла Р путем вращения вокруг прямой уровня плоскости угла, образованного прямой l и перпендикуляром и, остается дополнить его до прямого угла. Этот дополнительный угол и даст истинную величину угла а между прямой l и плоскостью 0.

Истинная величина двугранного угла — между двумя плоскостями Q и л. — может быть определена или путем замены плоскости проекций с целью преобразования ребра двугранного угла в проецирующую прямую (задачи 1 и 2), или если ребро не задано, как угол между двумя перпендикулярами n¹ и n², проведенными к данным плоскостям (см. § 61) из произвольной точки М пространства (см. рис. 145). В плоскости этих перпендикуляров при точке М получаем два плоских

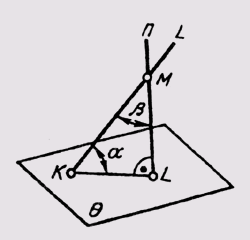
Рис. 144

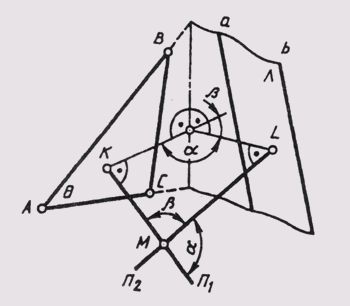
Рис. 145

угла а и Р, которые соответственно равны линейным углам двух смежных углов (двугранных), образованных плоскостями q и л,. Определив истинную величину углов между перпендикулярными n¹ и n² путем вращения вокруг прямой уровня, тем самым определим и линейный угол двугранного угла, образованного плоскостями q и л.

Для двух плоскостей возможны следующие варианты взаимного расположения: они параллельны или пересекаются по прямой линии. Из стереометрии известно, что две плоскости параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости. Это условие называют признаком параллельности плоскостей.