Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Использование процедур в приближенных вычислениях.

Пусть требуется вычислить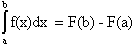

Значение 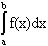равно площади криволинейной трапеции ACDB, сторона CD которой является частью графика функции f (x).

1 способ: преобразуем криволинейную трапецию в обычную, заменив сторону CD отрезком.

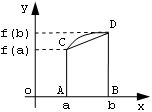
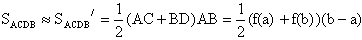
2 способ: заменим сторону CD криволинейной трапеции на отрезок, параллельный стороне AB и проходящий через одну из вершин C или D.

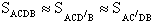
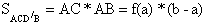
3 способ: восстановим в середине отрезка AB перпендикуляр до пересечения с графиком функции f(x). Проведем через найденную точку отрезок, параллельный AB.

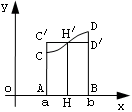
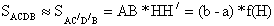
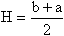
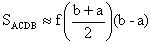
Для нахождения приближенного значения определенного интеграла разобъем отрезок AB на две равные части (величину 2 обозначим через n). В середине каждого отрезка восстановим перпендикуляры и построим соответствующие прямоугольники. Вычислим площадь S₁.

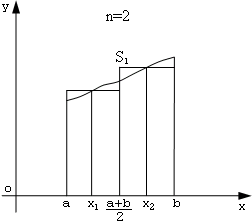
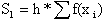
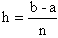
Т.к. выполнив вычисления один раз не возможно оценить их точность, то продолжим разбиение отрезка AB (n=4).

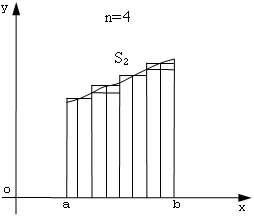
После проведенных вычислений можно оценить полученную точность, которая равна |S₁-S₂|. Если точность оказывается достаточной, то последнее вычисленное значение S₂ будет считаться значением определенного интеграла. Если точность не достаточна, то последнее разбиение считается начальным, т.е. S₁=S₂ и количество разбиений увеличивается вдвое, т.е. n=2*n.