Обратные тригонометрические функции

💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Определения. Многозначность и главные значения

Соотношение x = sin y позволяет найти как x по заданному y, так и y по заданному x (при | x |

 1). Таким образом, можно рассматривать не только синус как функцию угла, но и угол – как функцию синуса. Этот факт может быть записан как: y = arcsin x (“arcsin” читается “арксинус”).Например, вместо 1/2 = sin 30 можно записать: 30    arcsin 1/2. При второй форме записи угол обычно представляется в радианах:

 6 = arcsin1/2.

Определения. arcsin x – это угол, синус которого равен x. Аналогично определяются функции arccos x, arctan x, arccot x, arcsec x, arccosec x. Эти функции являются обратными по отношению к функциям sin x, cos x, tan x, cot x, sec x, cosec x, поэтому они называются обратными тригонометрическими функциями. Все обратные тригонометрические функции являются многозначными функциями, то есть каждому значению аргумента соответствует бесчисленное множество значений функции. Так, например, углы 30, 150, 390  510   750  имеют один и тот же синус.

Главное значение arcsin x – это его значение, которое находится между  

   2 и +

   2 ( 90 и + 90), включая границы:

Главное значение arccos x – это его значение, которое находится между 0 и

(0 и + 180), включая границы:

Главное значение arctan x – это его значение, которое находится между  

   2 и +

   2 ( 90 и + 90) без границ:

Главное значение arccot x – это его значение, которое находится между 0 и

(0 и + 180) без границ:

Если обозначить любое из значений обратных тригонометрических функций через Arcsin x, Arccos x, Arctan x, Arccot x и сохранить обозначения: arcsin x, arcos x, arctan x, arccot x для их главных значений, то связь между ними выражается следующими соотношениями:

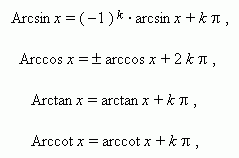
где k – любое целое число. При k = 0 мы имеем главные значения.