Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Исследование тригонометрических функций

I.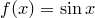

1) Область определения — .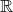

2) Множество значений — .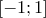

Доказательство. Множество значений функции 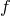есть множество ординат точек числовой окружности.

3) Функция строго возрастает на любом промежутке вида 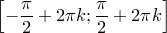, , 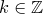строго убывает на любом отрезке вида , .

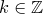Доказательство. Пусть 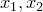— две точки такого промежутка, .

Следовательно, .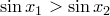

4) График — синусоида.

5) — главный период.

6) Корни .

II.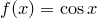

1) Область определения — .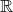

2) Множество значений — .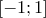

Доказательство. Множество значений функции 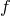есть множество абсцисс точек числовой окружности.

3) Функция строго убывает на любом промежутке вида , , 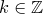строго возрастает на любом отрезке вида , .

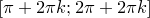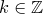Доказательство. Пусть 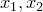— две точки такого промежутка, .

Следовательно, .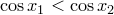

4) График — синусоида.

5) — главный период.

6) Корни .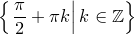

III.

1) Область определения — .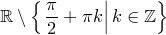

2) Множество значений — .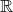

Лемма.

Рис. 44

Если точка не лежит на оси ординат, то точка пересечения прямой 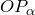с прямой 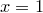имеет координаты .

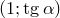Доказательство. Воспользуемся рисунком (см. рис. 44). Опустим из точки перпендикуляр на ось . Пусть он пересечет ось в точке 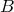. Треугольник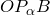и и 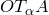подобны. Координаты точки — , точки — . Отсюда

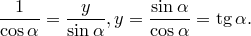
Определение. Прямая 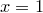называется линией тангенсов.

Рис. 45

Воспользуемся рисунком (рис. 45). Пусть 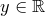. Докажем, что 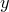является значением тангенса. Для этого найдем на линии тангенсов точку с ординатой 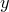и обозначим через 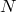какую-либо точку пересечения прямой 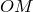с числовой окружностью. Пусть 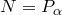. Тогда .

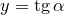3) Функция строго возрастает на любом промежутке вида , .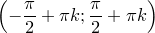

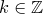Доказательство. Пусть 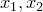— две точки такого промежутка, .

Если четно, то . Если нечетно, то 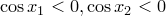.Следовательно, .

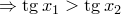4) График — тангенсоида.

5) 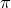— главный период.

6) Корни тангенса совпадают с корнями синуса.

На рис. 46 приведен график функции .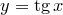

Рис. 46

На рис. 47 приведен график функции .

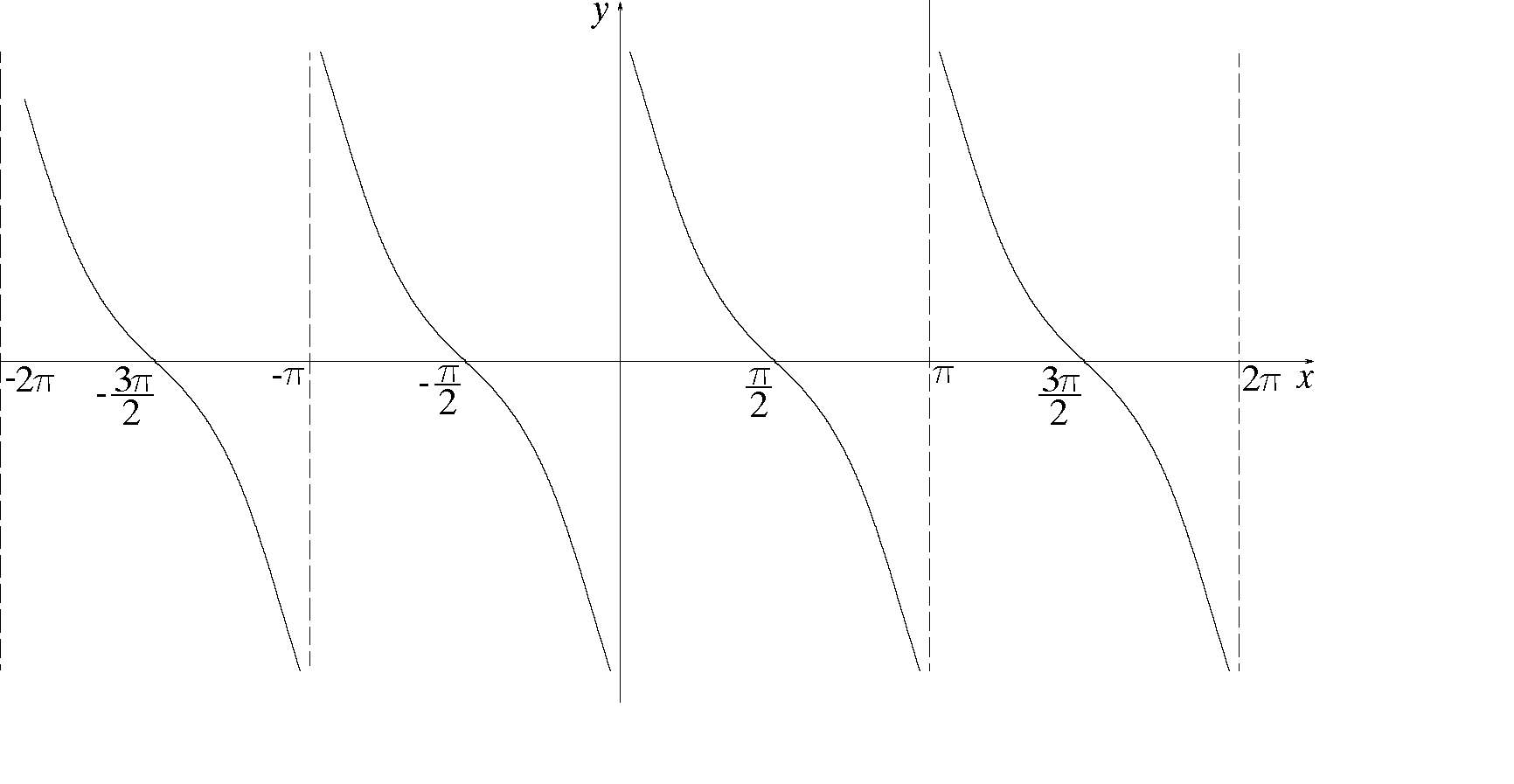
Рис. 47