Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Закон Ома. Сопротивление проводников

Немецкий физик Георг Ом (1787-1854) экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, в котором не действуют сторонние силы), пропорциональна напряжению U на концах проводника:

I = 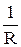U. (18.1)

где R - электрическое сопротивление проводника.

Уравнение (18.1) выражает закон Ома для однородного участка цепи. Единицей сопротивления служит Ом, равный сопротивлению такого проводника, в котором при напряжении 1 В течет ток силой 1 А. Величина, обратная сопротивлению

G = 1/R,

называется электрической проводимостьюпроводника. Единица проводимости сименс (См): 1 См — проводимость участка электрической цепи сопротивлением 1 Ом.

Сопротивление проводника зависит от его размеров и формы, а также от свойств материала, из которого он изготовлен. Для однородного цилиндрического проводника сопротивление R прямо пропор­ционально его длине l и обратно пропорционально площади его поперечного сечения S:

R = r , (18.2)

где r - коэффициент пропорциональности, характеризующий свойства материала проводника.

Коэффициент r называется удельным электрическим сопротивлением вещества. Единица удельного электрического сопротивления - Ом-метр (Ом× м). Наименьшим удельным сопротивлением обладают серебро (1, 6× 10^-8 Ом× м) и медь (1, 7× 10^-8Ом× м). На практике наряду с медными применяются алюминиевые провода. Хотя алюминий и имеет большее, чем медь, удельное сопротивление (2, 6× 10^-8 Ом× м), но зато обладает меньшей плотностью по сравнению с медью.

Найдем связь между векторами плотности тока 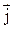и напряженности 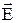в одной и той же точке проводника. В изотропном проводнике упорядоченное движение положительных носителей тока происходит в направлении вектора 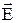. Поэтому направление векторов 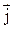и 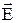совпадают. Выделим мысленно в окрестности некоторой точки элементарный цилиндрический объем с образующими, параллельными векторам 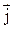и 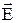(рисунок 21). Через поперечное сечение цилиндра течет ток силой jdS. Напряжение, приложенное к цилиндру, равно Edl, где Е - напряженность поля в данном месте, dl – высота цилиндра. Наконец, сопротивление цилиндра, согласно (18.2), равно r(dl/dS). Подставив эти значения в формулу (18.1), придем к соотношению:

jdS = Edl или j = .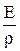

Воспользовавшись тем, что векторы 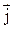и 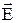имеют одинаковое направление, можно написать

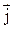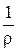
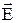= = s 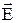. (18.3)

Формула (18.3) выражает закон Ома в дифференциальной форме. Обратная r величина s называется удельной электрической проводимостью материала. Единица, обратная Ому, называется сименсом (См). Соответственно единицей s является сименс на метр (См/м). Это соотношение справедливо и для переменных полей.

Допустим для простоты, что в проводнике имеются носители лишь одного знака. Согласно формуле (16.5) плотность тока в этом случае равна

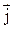= n e 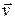. (18.4)

Сравнение этого выражения с формулой (18.3) приводит к заключению, что скорость упорядоченного движения носителей тока пропорциональна напряженности поля 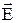, т.е. силе, сообщающей носителям упорядоченное движение. Пропорциональность скорости приложенной к телу силе наблюдается в тех случаях, когда кроме силы, вызвавшей движение, на тело действует сила сопротивления среды. Эта сила вызывается взаимодействием носителей тока с частицами, из которых построено вещество проводника. Наличие силы сопротивления упорядоченному движению носителей тока обусловливает электрическое сопротивление проводника.

Способность вещества проводить электрический ток характеризуется его удельным сопротивлением r или удельной проводимостью s. Эти величины определяются химической природой вещества и внешними условиями, в частности температурой, при которых оно находится.

Если в закон Ома для однородного участка цепи I = U/R (18.1) подставим выражение (17.6) для напряжения U = j₁ - j₂ + E, действующего на этом участке, то получаем соотношение

I = 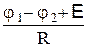или j₁ - j₂ + E = IR, (18.5)

выражающее закон Ома для неоднородного участка цепи (обобщенный закон Ома).

На примере схем, приведенных на рисунке 22, можно рассмотреть примеры использования обобщенного закона Ома. На схеме (а) вольтметр, подключенный к точкам 1 и 2 цепи, покажет напряжение j₁ - j₂. Так как клемма «+» источника присоединена со стороны точки 1, то, если бы в цепи ток отсутствовал, точка 1 находилась бы под более положительным потенциалом в сравнении с потенциалом точки 2, поэтому в последнем равенстве слагаемое Е необходимо брать со знаком «+». В схеме (а) ток течет от точки 2 к точке 1, поэтому слагаемое IR нужно брать со знаком «-». В итоге, в схеме (а) вольтметр, подключенный к точкам 1 и 2, покажет напряжение: j₁ - j₂ = Е - IR.

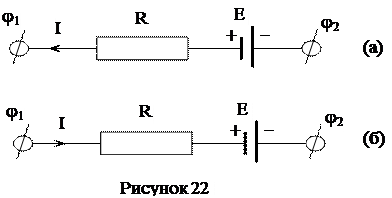В схеме (б) ток течет навстречу ЭДС, это возможно в том случае, когда к рассматриваемому участку цепи подключен источник тока с ЭДС, большей ЭДС данного участка. Такую схему включения используют при зарядке аккумуляторной батареи. В схеме (б) вольтметр, подключенный к точкам 1 и 2, покажет напряжение: j₁ - j₂ = Е + IR.

Если на данном участке цепи источник тока отсутствует (Е = 0), то из (18.5) приходим к закону Ома для однородного участка цепи (18.1):

I = 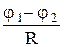= . (18.1)

Если же электрическая цепь замкнута, то выбранные точки 1 и 2 совпадают, и j₁ = j₂; тогда из (18.5) получаем выражение для закона Ома для замкнутой (полной) цепи:

I = ,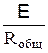

где E - ЭДС, действующая в цепи, R_общ - суммарное (общее) сопротивление всей цепи.

В общем случае R_общ = r + R, где r - внутреннее сопротивление источника тока, R - сопротивление внешней цепи. Поэтому закон Ома для замкнутой цепи будет иметь вид

I = . (18.6)

Если цепь разомкнута и, следовательно, в ней ток отсутствует (I = 0), то из закона Ома для неоднородного участка цепи (18.5) получим, что Е = j₁ - j₂, т. е. ЭДС, действующая в разомкнутой цепи, равна разности потенциалов на ее концах. Следовательно, для того, чтобы найти ЭДС источника тока, надо измерить разность потенциалов на его клеммах при разомкнутой цепи.

Закон Ома для полной цепи можно представить и в форме

Е = I (R + r) = I R + I r = U_R + U_r, (18.7)

и сформулировать его следующим образом: в замкнутой цепи постоянного тока ЭДС источника тока равна сумме падений напряжений на внешней и внутренней частях цепи. Величину U_R = I R, равную напряжению на внешней нагрузке, называют напряжением на клеммах источника. Замкнутую цепь в простейшем случае изображают так, как она представлена на рисунке 23. Если приведенная на рисунке 23 цепь разомкнута, то R®¥, а сила тока в цепи I = 0, и Е = U_R, т.е. напряжение на полюсах источника тока при разомкнутой цепи равно ЭДС источника тока.

Если клеммы источника Е в приведенной на рисунке 23 цепи закоротить, т.е. замкнуть между собой, то мы имеем случай так называемого короткого замыкания. При коротком замыкании источника сопротивление внешней цепи R = 0, и в случае незначительного внутреннего сопротивления r источника тока сила тока короткого замыкания I_кз, равная

I_кз = 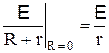, (18.8)

может оказаться значительной и привести к разрушению источника тока.