Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Конденсаторы

Как видно из § 3.12, для того, чтобы проводник обладал большой емкостью, он должен иметь очень большие размеры. На практике, однако, необходимы устройства, обладающие способностью при малых размерах и небольших относительно окружающих тел потенциалах накапливать значительные по величине заряды, иными словами, обладать большой емкостью. Эти устройства получили название конденсаторов.

Рассмотрим два проводника, между которыми существует электрическое напряжение U=j₁ - j₂, и предположим, что все линии вектора 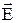, исходящие из одного проводника, заканчиваются на другом. Такую пару проводников называют простым конденсатором или просто конденсатором. Простым конденсатором, например, является плоский конденсатор, состоящий из двух параллельных проводящих пластин, если расстояние между пластинами мало по сравнению с их размерами. Оба проводника, образующие конденсатор, называются его обкладками. Так как силовые линии начинаются и заканчиваются на зарядах, то отсюда следует, что заряды, находящиеся на обкладках простого конденсатора, всегда равны по величине и противоположны по знаку.

Напряженность поля в любой точке между обкладками конденсатора всегда пропорциональна величине заряда обкладок. Поэтому согласно (4.18) и напряжение U между обкладками всегда пропорционально заряду обкладок q:

q = CU. (13.1)

Коэффициент пропорциональности С в этой формуле называют электрической емкостью конденсатора или просто его емкостью. Единица электроемкости - фарад(Ф): 1Ф - емкость такого конденсатора, у которого при заряде на каждой обкладке в 1 Кл напряжение между обкладками равно 1 В:

1 Ф = 1 .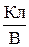

Емкость конденсатора зависит от его размеров, формы и от свойств среды, находящейся между его обкладками.

Пусть С₀ - емкость любого конденсатора, когда его обкладки находятся в вакууме. Практически мы получим ту же емкость, если между обкладками будет атмосферный воздух. Пусть далее С – емкость того же конденсатора, если все пространство между его обкладками заполнено каким-либо другим однородным изолятором. Отношение

С/С₀ = e (13.2)

называют диэлектрической проницаемостью изолятора. Из (13.2) вытекает, что емкость С конденсаторов любой формы прямо пропорциональна диэлектрической проницаемости e диэлектрика, заполняющего пространство между обкладками. Поэтому применение в качестве прослойки сегнетоэлектриков (e достигает ~ 10⁴) значительно увеличивает емкость конденсаторов.

Плоский конденсатор состоит из двух параллельных металлических пластин площадью S каждая, расположенных на расстоянии d, друг от друга, малом по сравнению с размерами пластин. Емкость плоского конденсатора определяется соотношением:

С = , (13.3)

где e - диэлектрическая проницаемость вещества, заполняющего зазор между пластинами конденсатора.

Электрическое поле между электродами плоского конденсатора является однородным (если пренебречь краевыми эффектами).

Цилиндрический конденсатор состоит из двух коаксиальных цилиндров с радиусами R (внешний) и r (внутренний). Длину цилиндров L будем считать весьма большой по сравнению с зазором между ними. Емкость цилиндрического конденсатора определяется соотношением:

С = 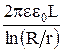. (13.4)

Сферический конденсатор состоит из двух проводников в виде концентрических сфер, разделенных сферическим слоем диэлектрика. Емкость сферического конденсатора определяется соотношением:

С = 4pee₀ 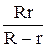, (13.5)

где R и r радиусы внешней и внутренней обкладок.

Двухпроводная линия представляет собой два параллельных цилиндрических провода с радиусами r и расстоянием между осями проводов d (d> > r). Будем считать, что все окружающие тела, включая и Землю, находятся на расстояниях, больших по сравнению с d, и поэтому будем считать оба провода как простой конденсатор. Емкость двухпроводной линии определяется соотношением:

С = 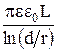, (13.6)

где L – длина двухпроводной линии.

Кроме емкости каждый конденсатор характеризуется предельным напряжением (напряжением пробоя), которое можно прикладывать к обкладкам конденсатора, не опасаясь его пробоя. При более высоком напряжении происходит электрический пробой и диэлектрик разрушается, т.е. конденсатор выходит из строя. Напряжение пробоя зависит от формы обкладок, свойств диэлектрика и его толщины.