
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Условия на границе раздела двух диэлектрических сред
|
|
Рассмотрим связь между векторами  и
и  на границе раздела двух однородных изотропных диэлектриков (диэлектрические проницаемости которых e1 и e2) при отсутствии на границе свободных зарядов. Искомые условия получим с помощью теоремы о циркуляции вектора
на границе раздела двух однородных изотропных диэлектриков (диэлектрические проницаемости которых e1 и e2) при отсутствии на границе свободных зарядов. Искомые условия получим с помощью теоремы о циркуляции вектора  (см. 4.5) и теоремы Остроградского – Гаусса для вектора
(см. 4.5) и теоремы Остроградского – Гаусса для вектора  (см. 9.4):
(см. 9.4):
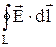 =
= 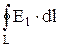 = 0,
= 0,  =
= 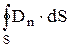 =
= 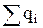 =0.
=0.

Возьмем небольшой прямоугольный контур сторонами, параллельными границе раздела и такой длины a, чтобы в ее пределах напряженность поля  в каждом диэлектрике можно было считать одинаковой, и пренебрежимо малой высотой b. Контур частично проходит в первом диэлектрике, частично – во втором. Ось х проходит через середину стороны b (см. рисунок 15).
в каждом диэлектрике можно было считать одинаковой, и пренебрежимо малой высотой b. Контур частично проходит в первом диэлектрике, частично – во втором. Ось х проходит через середину стороны b (см. рисунок 15).
Пусть в диэлектриках создано поле, напряженность которого в первом диэлектрике равна 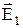 , а во втором -
, а во втором -  . Циркуляция вектора
. Циркуляция вектора  по выбранному нами контуру должна быть равна нулю. При указанном направлении обхода циркуляция вектора
по выбранному нами контуру должна быть равна нулю. При указанном направлении обхода циркуляция вектора  может быть представлена в виде
может быть представлена в виде
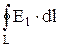 = Е1 х × а - Е2 х × а + Е b × 2 b, (9.5)
= Е1 х × а - Е2 х × а + Е b × 2 b, (9.5)
где Е b – среднее значение Еl на перпендикулярных к границе участках контура.
Тогда
(Е2 х - Е1 х ) а = Е b × 2 b.
В пределе при стремящейся к нулю ширине контура b получается равенство
Е1 х =Е2 х . (9.6)
Значения проекций векторов 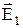 и
и  на ось х берутся в непосредственной близости к границе диэлектриков.
на ось х берутся в непосредственной близости к границе диэлектриков.
Соотношение (9.6) выполняется при произвольном выборе оси х; нужно лишь, чтобы эта ось лежала в плоскости раздела диэлектриков. Из (9.6) следует, что при таком выборе оси х, при котором Е1 х = 0, проекция вектора Е2 х также будет равна нулю. Это означает, что векторы 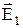 и
и  в двух близких точках, взятых по разные стороны границы, лежат в одной плоскости с нормалью к поверхности раздела. Представим каждый из векторов
в двух близких точках, взятых по разные стороны границы, лежат в одной плоскости с нормалью к поверхности раздела. Представим каждый из векторов 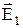 и
и  в виде суммы нормальной и тангенциальной составляющих:
в виде суммы нормальной и тангенциальной составляющих:
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
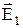 =
= 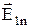 +
+  ;
;  =
= 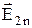 +
+ 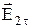 . (9.7)
. (9.7)
В соответствии с (9.6)
Е1t = Е2t, (9.8)
т.е. тангенциальные составляющие вектора  оказываются одинаковыми по обе стороны границы раздела. В (9.8) Е1t и Е2t - проекции векторов
оказываются одинаковыми по обе стороны границы раздела. В (9.8) Е1t и Е2t - проекции векторов 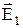 и
и  на единичный вектор
на единичный вектор 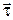 , направленный вдоль линии пересечения плоскости раздела диэлектриков с плоскостью, в которой лежат вектора
, направленный вдоль линии пересечения плоскости раздела диэлектриков с плоскостью, в которой лежат вектора 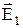 и
и  .
.
Заменив, согласно (9.1), проекции вектора 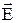 проекциями вектора
проекциями вектора  , деленными на ee0, получим из (9.8) соотношение
, деленными на ee0, получим из (9.8) соотношение
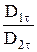 =
= 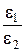 . (9.9)
. (9.9)
 На границе раздела двух диэлектриков (рисунок 16) построим прямую цилиндрическую поверхность ничтожно малой высоты h, одно основание S1 которой находится в первом диэлектрике, другое основание S2 находится во втором. Оба основания одинаковы (S1 = S2 = S) и настолько малы, что в пределах каждого из них поле можно считать однородным. Применим к этой поверхности теорему Остроградского – Гаусса. Так как на границе между диэлектриками зарядов нет, правая часть в (9.4) равна нулю.
На границе раздела двух диэлектриков (рисунок 16) построим прямую цилиндрическую поверхность ничтожно малой высоты h, одно основание S1 которой находится в первом диэлектрике, другое основание S2 находится во втором. Оба основания одинаковы (S1 = S2 = S) и настолько малы, что в пределах каждого из них поле можно считать однородным. Применим к этой поверхности теорему Остроградского – Гаусса. Так как на границе между диэлектриками зарядов нет, правая часть в (9.4) равна нулю.
Поток через основание S1 равен D1nS, где D1n - проекция вектора  в первом диэлектрике на нормаль
в первом диэлектрике на нормаль 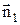 . Аналогично поток через основание S2 равен D2nS, где D2n - проекция вектора
. Аналогично поток через основание S2 равен D2nS, где D2n - проекция вектора  во втором диэлектрике на нормаль
во втором диэлектрике на нормаль 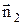 . Поток через боковую поверхность можно представить в виде DnSбок, где Dn – значение электрического смещения, усредненное по всей боковой поверхности, Sбок – значение этой поверхности. Таким образом, можно записать
. Поток через боковую поверхность можно представить в виде DnSбок, где Dn – значение электрического смещения, усредненное по всей боковой поверхности, Sбок – значение этой поверхности. Таким образом, можно записать
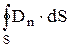 = D1nS + D2nS + DnSбок = 0. (9.10)
= D1nS + D2nS + DnSбок = 0. (9.10)
Если устремить высоту цилиндра h к нулю, Sбок также будет стремиться к нулю. Поэтому в пределе соотношение (9.10) примет вид
D1n = - D2n.
Знаки проекций оказались разными вследствие того, что нормали 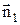 и
и 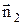 к основаниям цилиндра имеют противоположные направления. Если проецировать
к основаниям цилиндра имеют противоположные направления. Если проецировать  и
и  на одну и ту же нормаль, получится условие
на одну и ту же нормаль, получится условие
D1n = D2n, (9.11)
т.е. нормальные составляющие вектора  оказываются одинаковыми по разные стороны границы раздела двух диэлектриков.
оказываются одинаковыми по разные стороны границы раздела двух диэлектриков.
Заменив согласно (9.1) проекции вектора  проекциями вектора
проекциями вектора 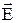 , умноженными на ee0, получим соотношение
, умноженными на ee0, получим соотношение
e1e0Е1n = e2e0Е2n,
из которого следует, что
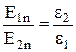 . (9.12)
. (9.12)
Таким образом, при переходе через границу раздела двух диэлектрических сред тангенциальная составляющая вектора 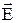 (
(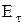 ) и нормальная составляющая вектора
) и нормальная составляющая вектора  (
(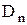 ) изменяются непрерывно (не претерпевают скачка), а нормальная составляющая вектора
) изменяются непрерывно (не претерпевают скачка), а нормальная составляющая вектора 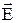 (
(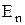 ) и тангенциальная составляющая вектора
) и тангенциальная составляющая вектора  (
(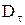 ) претерпевают скачок.
) претерпевают скачок.
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
Соотношения (9.8), (9.9), (9.11) и (9.12) определяют условия, которым должны удовлетворять векторы 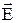 и
и  на границе двух диэлектриков в случае, если на этой границе нет сторонних зарядов. Мы получили эти соотношения для электростатического поля. Однако они справедливы и для полей, изменяющихся со временем.
на границе двух диэлектриков в случае, если на этой границе нет сторонних зарядов. Мы получили эти соотношения для электростатического поля. Однако они справедливы и для полей, изменяющихся со временем.
 Найденные нами условия справедливы и для границы раздела диэлектрика с вакуумом. В этом случае одну из диэлектрических проницаемостей нужно положить равной единице.
Найденные нами условия справедливы и для границы раздела диэлектрика с вакуумом. В этом случае одну из диэлектрических проницаемостей нужно положить равной единице.
Из полученных условий для составляющих векторов 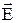 и
и  на границе раздела двух диэлектриков следует, что линии этих векторов испытывают на этой границе излом, т.е. преломляются. Найдем соотношение между углами преломления a1 и a2 (см. рисунок 17):
на границе раздела двух диэлектриков следует, что линии этих векторов испытывают на этой границе излом, т.е. преломляются. Найдем соотношение между углами преломления a1 и a2 (см. рисунок 17):
 ,
,
откуда с учетом (9.9) и (9.11) получается закон преломления линий вектора электрического смещения  :
:
 . (9.13)
. (9.13)
При входе в диэлектрик с большей e линии  удаляются от нормали, и, наоборот, при входе в диэлектрик с меньшей e угол, образуемый линиями
удаляются от нормали, и, наоборот, при входе в диэлектрик с меньшей e угол, образуемый линиями  с нормалью, уменьшается.
с нормалью, уменьшается.
Закон преломления силовых линий (линий 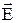 ) в изотропных диэлектриках, очевидно, такой же, как и закон преломления линий смещения
) в изотропных диэлектриках, очевидно, такой же, как и закон преломления линий смещения  , так как в каждом из диэлектриков направления векторов
, так как в каждом из диэлектриков направления векторов 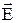 и
и  совпадают. Однако картины линий смещения и силовых линий будут все же различны. Различие заключается в том, что линии смещения непрерывны, в то время как часть силовых линий прерывается на границе раздела (см. § 2.8).
совпадают. Однако картины линий смещения и силовых линий будут все же различны. Различие заключается в том, что линии смещения непрерывны, в то время как часть силовых линий прерывается на границе раздела (см. § 2.8).
|
|
