Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Матричный метод решения СЛАУ

Рассмотрим СЛАУ, в которой число уравнений совпадает с числом неизвестных, и запишем ее в виде . Если определитель основной матрицы этой системы отличен от 0, то существует обратная матрица 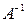, причем . Умножим обе части равенства слева на 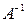и получим равенство 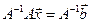. Так как первые 2 сомножителя в левой части этого уравнения равны единичной матрице и тем самым сокращаются, то мы приходим к формуле

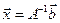. (2)

В качестве примера решения системы матричным методом можно рассматривать пример 2 из предыдущей лекции.

Заметим, что рассмотренные методы – Крамера и матричный не являются универсальными методами. Их можно применять только в том случае, когда число уравнений и число неизвестных совпадают, и определитель основной матрицы не равен 0.