Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Точность коэффициентов регрессии. Доверительные интервалы

Оценки коэффициентов регрессии зависят от используемой выборки значений переменных x и y и являются случайными величинами. Для характеристики точности полученных оценок можно использовать стандартные ошибки коэффициентов регрессии.

Под стандартной ошибкой коэффициента регрессии понимается оценка стандартного отклонения функции плотности вероятности данного коэффициента.

Стандартные ошибки коэффициентов регрессии s_bi определяются соотношениями

, (26) где s²_ост представляет собой несмещенную оценку остаточной дисперсии

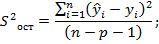
- диагональный элемент матрицы .

Величину можно вычислить как

,

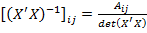где Aij - алгебраическое дополнение к элементу ij матрицы X¢ X).

Сопоставляя оценки параметров и их стандартные ошибки, можно сделать вывод о надежности (точности) полученных оценок. Для оценки статистической значимости коэффициентов регрессии применяется t-критерий Стьюдента, основанный на том факте, что отношения

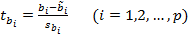(27) являются t-статистиками, т. е. случайными величинами, распределенными по закону Стьюдента с числом степеней свободы n-p-1. Через 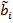обозначены точные значения коэффициентов регрессии.

Согласно t-критерию Стьюдента, выдвигается «нулевая» гипотеза H0 о статистической незначимости коэффициента уравнения регрессии (т. е. о статистически незначимом отличии величины а или b_i от нуля). Эта гипотеза отвергается при выполнении условия t > t_крит, где t_крит определяется по таблицам t-критерия Стьюдента по числу степеней свободы k₁ = n-p-1 (p - число независимых переменных в уравнении регрессии) и заданному уровню значимости α.

t-критерий Стьюдента применяется в процедуре принятия решения о целесообразности включения фактора в модель. Если коэффициент при факторе в уравнении регрессии оказывается незначимым, то включать данный фактор в модель не рекомендуется. Отметим, что это правило не является абсолютным и бывают ситуации, когда включение в модель статистически незначимого фактора определяется экономической целесообразностью.

Доверительные интервалы для параметров b_i уравнения линейной регрессии определяются соотношениями:

(28)

Величина t_{1-α, n-2} представляет собой табличное значение t-критерия Стьюдента на уровне значимости α при степени свободы n–2.

Если в границы доверительного интервала попадает ноль, т. е. нижняя граница отрицательна, а верхняя положительна, то оцениваемый параметр принимается равным нулю, так как он не может одновременно принимать и положительное, и отрицательное значения.

Точность полученного уравнения регрессии можно оценить, анализируя доверительный интервал для функции регрессии, т. е. для среднего значения 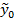, зависимой переменной y при заданных значениях объясняющих переменных x₁ = x₁₀, x₂ = x₂₀,..., x_p = x_p0.,

Доверительный интервал для функции регрессии определяется соотношениями

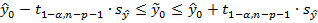, (29)

где 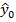– групповая средняя, определяемая по уравнению регрессии при заданных значениях объясняющих переменных x₁ = x₁₀, x₂ = x₂₀,..., x_p = x_p0;

– ее стандартная ошибка; (30)

ỹ ₀ – точное значение групповой средней; X₀ – вектор, составленный из заданных значений независимых переменных X₀ = (1, x₁₀, x₂₀,..., x_p0 ).

Доверительный интервал для индивидуальных значений зависимой переменной y^*₀ определяется соотношениями

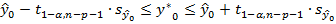(31)

где

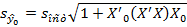(32)

есть стандартная ошибка индивидуальных значений зависимой переменной y^*₀.

Контрольные вопросы

1. Что понимается под множественной регрессией?

2. Какие задачи решаются при построении уравнения регрессии?

3. Какие задачи решаются при спецификации модели?

4. Какие требования предъявляются к факторам, включаемым в уравнение регрессии?

5. Какие функции чаще используются для построения уравнения множественной регрессии?

6. Какой вид имеет система нормальных уравнений метода наименьших квадратов в случае линейной регрессии?

7. Как проверяется значимость уравнения регрессии и его коэффициентов?

8. Что такое стандартизированные переменные?

10. Как оценивается значимость факторов?

11. Каковы последствия неправильной спецификации модели?

12. К чему приводит отсутствие в уравнении существенной независимой переменной?