Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Вынужденные колебания.

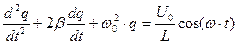
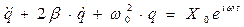
Общее решение неоднородного дифференциального уравнения есть сумма частного решения неоднородного уравнения и общего решения однородного уравнения. Частное решение ищем в следующем виде 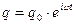. Произведя дифференцирование, получим:

.

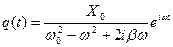Общее решение может быть записано в виде:

.

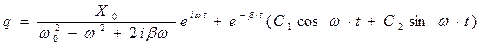Выбором постоянных C₁ и C₂ можно удовлетворить любым начальным условиям.

Представим знаменатель в показательной форме:

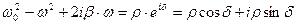. Тогда 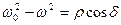и 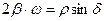, что позволяет выразить

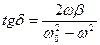и .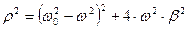

При 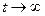свободные колебания практически совсем затухнут и останутся лишь вынужденные колебания 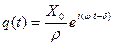. В вещественной форме

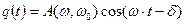, где

.

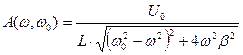Таким образом, мы определили, что амплитуда вынужденных колебаний зависит от частоты поданного синусоидального напряжения. При 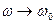амплитуда резко возрастает. Это явление называется резонансом. Определим, при какой частоте амплитуда достигает максимума. Очевидно, это происходит тогда, когда знаменатель принимает минимальное значение. По правилам поиска экстремума функции ищем значения аргумента, при котором производная равна нулю.

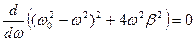. То есть 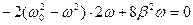. Отсюда .

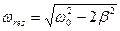Мощность.

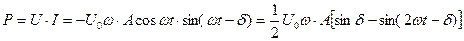
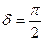то есть .

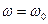Ширина резонансной кривой. Найдем значения частот слева и справа от резонанса, при которых 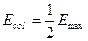. Эти частоты удовлетворяют условиям 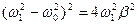и .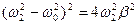

При условии, что 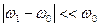и 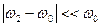с хорошей точностью можно получить.

.

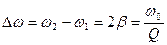Закон Ома для переменных (синусоидальных) токов.

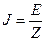
Комплексная величина 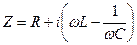называется импедансом.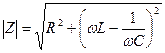

Сдвиг фаз между током и напряжением дается следующим выражением
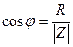