Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Теорема Гаусса.

Введем понятие потока вектора 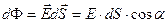. Рассмотрим поток через площадку 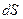, расположенную произвольным способом на расстоянии от точечного заряда q. Если мы разместим площадку 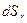на том же расстоянии, но перпендикулярно вектору напряженности, то выполняется соотношение 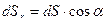. . 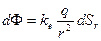Телесный угол, под которым видна площадка 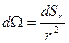. Обратите внимание, поток не зависит от того, как расположена площадка. Интегрируя по всей сфере, получим поток вектора напряженности для всей сферы, окружающей заряд 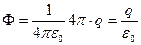. Любую систему зарядов можно представить, как состоящую из ряда точечных зарядов.

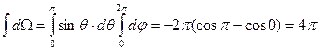
Сформулируем окончательно теорему Гаусса: поток вектора напряженности стационарного электрического поля через любую замкнутую поверхность равен сумме зарядов, находящихся внутри этой поверхности, деленной на электрическую постоянную.

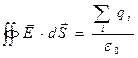
Под 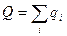здесь подразумевается сумма всех зарядов, расположенных внутри замкнутой поверхности. Теорема Гаусса связывает напряженность поля с источником – зарядами.

Рассмотрим случаи применения теоремы Гаусса.

Бесконечная заряженная плоскость.

Рассмотрим поле бесконечной положительно заряженной плоскости. Так как плоскость бесконечна, в любой точке напряженности поля одинаковы и перпендикулярны плоскости. Представим себе поверхность в виде параллелепипеда с площадью основания S. Поток напряженности через верхнюю и нижнюю грани равен 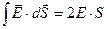. Поток напряженности через боковую поверхность равен нулю, так как вектор напряженности перпендикулярен вектору площади. С другой стороны, заряд внутри параллелепипеда равен 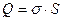. Подставляя эти соотношения в, получим . .

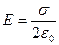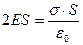Две бесконечные противоположно заряженные плоскости. Вне плоскостей E = 0. Между плоскостями напряженности поля от обоих плоскостей складываются.

.

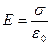Заряженная сфера (заряд Q и радиус сферы R). Окружим заряженную сферу воображаемой сферой радиусом r. Из соображений симметрии очевидно, что в любой точке вектор перпендикулярен поверхности сферы и интеграл равен 4π r²E. С другой стороны, по теореме Гаусса этот интеграл равен Q/ε ₀ при r > R и 0 при r < R. Отсюда 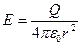при r > R и E = 0 при r < R.

Однородно заряженный шар. Выделим мысленно сферу внутри шара. Тогда по теореме Гаусса: 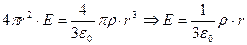. Где плотность заряда 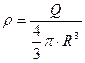. Окончательно получаем: ().

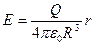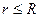Вне шара формула такая же, как для точечного заряда. Это легко доказать, окружив шар сферой радиусом 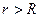и применить теорему Гаусса используя сферическую симметрию задачи.

Однородно заряженная нить.

Линейная плотность заряда λ. Окружим нить цилиндром радиусом r и длиной l. Поток напряженности через боковую поверхность равен: 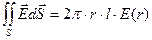. Поток через торцы равен нулю, поскольку вектор напряженности перпендикулярен нормали к поверхности. Применим теорему Гаусса.

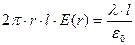. Отсюда .

_____________________

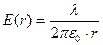Теорему Гаусса можно записать в дифференциальном виде.

Для того, чтобы преобразовать интеграл по поверхности, возьмем поверхность в виде кубика с гранями dx, dy, dz. Рассмотрим поток через грани, параллельные плоскости YZ:

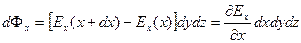
Аналогично и

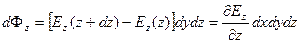
Используем теорему Гаусс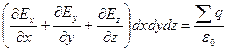а Плотность заряда

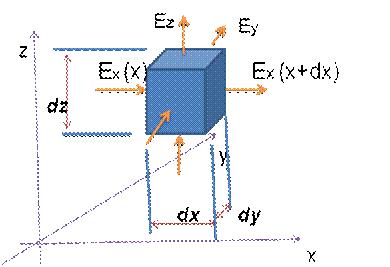
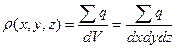
Введя обозначение 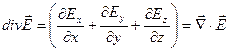, получим

.

С помощью оператора “набла”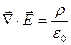