Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Примеры решения задач. Задача 1. В т. А экрана от источника S1 монохроматического света длиной волны l=0,5 мкм приходят два луча: непосредственно от источника лучей S1А

Задача 1. В т. А экрана от источника S₁ монохроматического света длиной волны l=0, 5 мкм приходят два луча: непосредственно от источника лучей S₁А, перпендикулярный экрану, и луч S₁ВА, отраженный в т. В от зеркала, параллельного лучу S₁А (рис. 3.3). Расстояние l ₁ экрана от источника равняется 1 м; расстояние h от луча S₁А к плоскости зеркала равняется 2 мм. Определить: 1) что будет наблюдаться в т. А экрана -усиление или ослабление интенсивности; 2) как изменится интенсивность в т. А, если на пути луча S₁А перпендикулярно нему разместить плоскопараллельную пластинку стекла (n=1, 55) толщиной 6 мкм.

Дано:

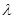=0, 5мкм==5∙ 10^-7 м

l ₁=1 м

h=2 мм==2∙ 10^-3 м

n=1, 55

d=6 мкм==6∙ 10^-6м

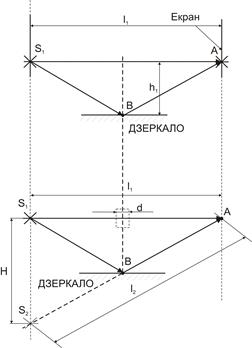
Рис.3.2

Рис. 3.3

Начертим мысленное изображение S₂ источника S₁ в зеркале (рис. 3.3). Источника S₁ и S₂ есть когерентными, поэтому при добавлении волн, которые приходят от этих источников на экран, возникает интерференционная картина. Усиление или ослабление интенсивности в той или другой точке экрана зависит от оптической разности хода интерферирующих лучей, то есть от числа m полуволн, которые укладываются на оптической разности хода:

m= Δ /(l/2) (1)

если m - целое четное, то интенсивность будет максимальной; если m - целое нечетное, то интенсивность минимальная. При дробном m или происходит частичное усиление (если m более близкое к четному числу), или частичное ослабление (если m -более близкое к нечетному числу).

1.Оптическая разность хода будет состоять из геометрической разности 2- 1 (оба луча идут в воздухе) и дополнительной разности хода l/2, обусловленной изменением фазы колебаний при отражении от среды оптически более плотной. Таким образом

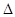₁= l ₁- l ₂+ l/2

поскольку l ₂= 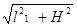(рис.3.3), тогда

l ₂- l ₁= l ₁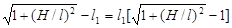

Величина H/ l ₁< < 1, поэтому для вычисления корня можно вычислить приближенной формулой

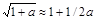при а < < 1

Применив ее, получим

l ₁- l ₂ 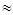l ₁[1+1/2(H/ l ₁₎²-1]=H²/2 l ²₁ откуда

₁=(H²/2 l ₁)+l /2 m₁=[(H²/2 l ₁)+ l/2]/l /2

Поскольку H==2h, тогда

m₁=(4h²/l₁l)+1=4∙ 4∙ 10^-6/1∙ 5∙ 10^-7=33

В точке А наблюдается минимум интенсивности.

2. Стеклянная пластина толщиной d, поставленная на пути луча S₁A (рис. 3.3), изменит оптическую длину пути. Теперь оптическая длина пути будет состоять из геометрической длины пути 1-d и оптической длины пути n∙ d в самой пластине, то есть

L=(l ₁-d)+nd= l ₁+(n-1) d

Оптическая разность хода лучей

Δ ₂= l ₁ - L+ 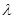/2= l ₂-[ l ₁+(n-1)d]+ l/2

или из формулы (1)

Δ ₂=Δ ₁-(n-1)d

m₂=Δ ₂/(l/2)= [Δ ₁-(n-1)d]/ (l/2)

m₂=33-[2∙ 6∙ 10^-6∙ (1.55-1)]/5∙ 10^-7=19.8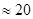

Число полуволн дробное, оно более близкое к четному числу 20. Итак, будет частичное усиление.

Ответ: 1) m₁=33 в точке А минимум интенсивности. 2) m₂=19, 8 в точке А усиление интенсивности света.

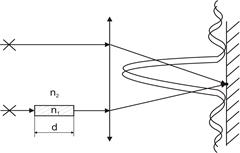
Задача 2. На тонкую пленку с показателем преломления n1= 1, 5 падает нормально параллельный пучок света длиной волны l =6∙ 10^-7 м Найти минимальную толщину пленки, при которой будет наблюдаться интерференция света в отраженных лучах.

n₁=1, 5

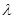=6∙ 10^-7 м

d_min-?

Рис. 3.4

Физическую систему составляет тонкая пленка и пучок световых волн (рис. 3.4). При падении световой волны на пленку происходит отображение ее от обеих поверхностей пленки. В результате возникают две световых волны 1', 1''. Оптическая разность хода, который приобретается лучами 1', 1'':

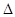=2АВ n₁-АДn₂ (1)

где n₁ - показатель преломления пленки, n₂ - показатель преломления среды, которая окружает пленку (n₂=1). Из рисунка 3.4 видно, что

АВ=d/cosr (2)

АД=АСsini=2dtgrsini (3)

На основе закона преломления света имеем:

sini/sinr=n₁/n₂=n₁ откуда

sini=n₁sinr (4)

Тогда выражение (1) можно записать в виде (2) - (4)

Δ ₁=2d

Необходимо учесть, что в т. А отражение происходит от оптически более плотной среды, поэтому фаза волны сменяется и к разности хода прибавляется l/2 (l - длина волны в вакууме), итак,

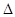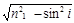=2d +l /2

Условие максимума в интерференционной картине можно записать

Δ _max=2m(l/2)=2d +l /2 (5)

где m - 1, 2, 3...-порядок интерференционного максимума. Для определения d_mіn необходимо в выражении (5) принять m=1. Поскольку параллельный пучок света падает нормально на пленку, то sіnі=0, тогда

2d_minn=l /2 d_min= l/4n₁=10^-7 м

Ответ: минимальная толщина пленки равняется 10^-7 м.

Задача 3. На экране наблюдается интерференционная картина в результате наложения лучей от двух когерентных источников с длиной волны (l =500 нм). На пути одного из лучей перпендикулярно ему поместили стеклянную пластинку (n₁=1, 6) толщиной d=5 мкм. Определить, на сколько полос сместится при этом интерференционная картина.

Дано:

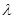=500 нм=5∙ 10^-7 м

n₁=1, 6

d=5 мкм=5∙ 10^-6 м

Δ m-?

Рис. 3.5

При внесении стеклянной пластинки оптическая разность хода между лучами (рис.3.5) изменится на

Δ =n₁d-n₂d

где n₂ - показатель преломления среды (n₂=1).

Внесение пластинки приведет к сдвигу интерференционной наказания-плетни на m полос, то есть дополнительная разность хода равняется m, тогда

Δ =d (n₁-1)=m₁l -m₂l =Δ ml

откуда

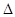m=d (n₁-1)/l =5∙ 10^-6∙ (1, 6-1)/5∙ 10^-6=6

Ответ: интерференционная картина сместится на 6 полос.

Задача 4. На стеклянный клин (n₁=1, 5) с преломляющим углом =40" нормально падает монохроматический свет с длиной волны =600 нм. Определить в интерференционной картине отстань между двумя соседними минимумами.

Дано:

n₁=1, 5

α =40’’=1, 94∙ 10^-4 рад

l=600 нм=6∙ 10^-7 м

b -?

Рис. 3.6

Параллельный пучок света, падая нормально к грани клина, отражается от его верхней и нижней грани (рис.3.6). Так как угол клина маленький, то отраженные лучи 1 и 2 практически параллельные. Отраженные лучи когерентные и на поверхности клина будут наблюдаться интерференционные полосы.

Условие минимума для клина в общем случае:

2dn₁cosr +l /2 =(2m+1)l /2 де m=0, 1, 2…

d-толщина клина в месте темной полосы, которая отвечает номеру m; r - угол преломления; l/2 - дополнительная разность хода, обусловленная отражения световой волны 1 от оптически более плотной среды. Угол падения и соответственно условию равняется нулю, итак, и угол преломления r=0, тогда

2dn₁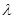₌ m

откуда

d=ml /2n₁ (1)

Из рисунка 3.6 вытекает, что

sinα =(d_m+1-d_m)/b (2)

Через малость угла sіnα, подставив (1) получим

α = [((m+1) l)-(ml)]/2n₁b=l /2bn₁

b=l /2n₁α =6*10^-7/2∙ 1.5∙ 1.94∙ 10^-4=1.03∙ 10^-3 м.

Ответ: отстань между двумя соседними минимумами 1, 03 мм.

Задача 5. Плосковыпуклая линза (n₁=1, 6) выпуклой стороной прижата к стеклянной пластинке. Расстояние между первыми двумя кольцами Ньютона, которые наблюдаются в отраженном свете, равняется 0, 5 мм. Определить оптическую силу линзы, если ее освещение происходит монохроматическим светом с l=550 нм, что падает нормально.

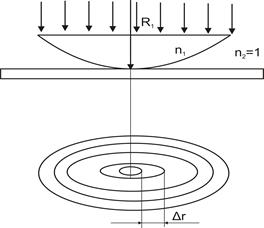Дано:

n₁=1, 6

Δ r₁=0.5 мм=5∙ 10^-4 м

l=550 нм=5, 5∙ 10^-7 м

D-?

Рис. 3.7

Оптическая сила линзы в общем случае

D=(N-1) (1/R₁+1/R₂)

где N - относительный показатель преломления (n₁ и n₂ - соответственно показатели преломление линзы и окружающей среды); R₁ и R₂ - радиусы кривизны поверхностей линзы. Так как линза плоско-выпуклая R₂=¥ и 1/R₂=0 тогда

D= (n₁-1)/ R₁ (1)

Для определения радиуса линзы воспользуемся выражениями для радиуса темного кольца Ньютона в отраженном свете (рис.3.7)

r_m = (m=0, 1, 2…)

где m - номер кольца.

Разность радиусов первых двух темных колец

Δ r₁₂=r₂-r₁=

откуда

R= 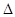r²₁₂/(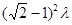

Подставив (2) в (1) получаем

D =(n₁-1) ()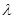

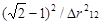D = (1, 6-1)∙ 5, 5∙ 10^-7(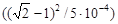 =0, 547 дптр

Ответ: оптическая линза 0, 547 дптр.

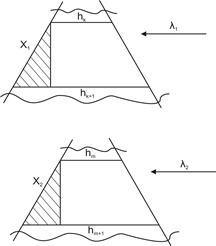
Задача 6. Сначала вертикальную мыльную пленку наблюдают в отраженном свете через красное стекло (l₁=6, 3∙ 10^-7 м). При этом расстояние между соседними красными полосами равняется 3 мм. Потом эту пленку наблюдают через синее стекло (l₂=4∙ 10^-7 м). Найти расстояние между соседними синими полосами. Считать, что форма пленки за время наблюдения не изменяется.

Дано:

l ₁=6, 3∙ 10^-7 м

l₂=4∙ 10^-7 м

х₁=3 мм=3∙ 10^-3 м

х₂-?

а)

б)

Рис.3.8

В глаз наблюдателя попадают лучи, отраженные от тонкого клина перпендикулярно его поверхности. Тогда для k-ї и (k+1)-ї красных полос оптические различия хода соответственно равные:

Δ _k=2h_kn -l/2;

Δ _kmax=kl₁

Δ _k+1=2h_k+1n-l /2;

Δ _k+1max=(k+1)l ₁

(cosr=1 угла преломления в обоих случаях)

где h_k и h_k+1 - соответствующие данным полосам толщины вертикальной мыльной пленки, пересечение которой клин (рисунок 3.8 а, б).

Δ _k+1-Δ _k=2h_k+1n-(l _1/2)-(2h_kn-(l _1/2)=(k+1) l₁-kl ₁

откуда

2n(h_k+1-h_k)= l₁, аналогично для синих полос.

2n (h_m+1-h_m)=l₂

Разделив почленно эти выражения, получим:

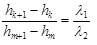
Из сходства заштрихованных треугольников (рис.3.8) вытекает:

х₁=х₂l ₁/2l

х₂₌3∙ 10^-3∙ 4∙ 10^-7/6, 3∙ 10^-7=1, 9∙ 10^-3 м.

Ответ: расстояние между соседними полосами 1мм